Joint factor analysis
DongyueXie
2021-09-12
Last updated: 2021-10-12
Checks: 7 0
Knit directory: SMF/
This reproducible R Markdown analysis was created with workflowr (version 1.6.2). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.
Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.
Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.
The command set.seed(20190719) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.
Great job! Recording the operating system, R version, and package versions is critical for reproducibility.
Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.
Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.
Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.
The results in this page were generated with repository version fc62fd8. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.
Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:
Ignored files:
Ignored: .DS_Store
Ignored: .Rhistory
Ignored: .Rproj.user/
Ignored: analysis/.DS_Store
Ignored: data/.DS_Store
Ignored: data/external_data/
Untracked files:
Untracked: analysis/sparse_smoothing.Rmd
Untracked: data/luis/
Untracked: output/flash_on_cmc2_reduced.rds
Untracked: output/flash_on_cmc2_reduced_2000kb.rds
Untracked: output/wave_flash_on_cmc2_reduced_2000kb.rds
Unstaged changes:
Modified: analysis/index.Rmd
Modified: analysis/luis_data.Rmd
Modified: analysis/smooth_flash.Rmd
Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.
These are the previous versions of the repository in which changes were made to the R Markdown (analysis/joint_factoranalysis.Rmd) and HTML (docs/joint_factoranalysis.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.
| File | Version | Author | Date | Message |
|---|---|---|---|---|
| Rmd | fc62fd8 | Dongyue Xie | 2021-10-12 | wflow_publish(“analysis/joint_factoranalysis.Rmd”) |
| Rmd | 03ceb24 | DongyueXie | 2021-10-11 | add |
Introduction
Here we study if the joint factor analysis could recover the co-varying pattern of the two functions.
Gaussian case
set.seed(123)
n = 120
p = 256
K= 3
L = matrix(rnorm(n*K),ncol=K)
FF = matrix(1, nrow=p, ncol=K)
FF[(p/8*1):(p/8*2),1] = 5
FF[(p/8*3):(p/8*4),2] = 5
FF[(p/8*5):(p/8*7),3] = 5
FFF = rbind(FF,FF)
s = 0.5
y = tcrossprod(L,FFF) + matrix(rnorm(n*p*2,0,s),nrow=n,ncol=p*2)
par(mfrow=c(3,1))
plot(FF[,1],type='l')
plot(FF[,2],type='l')
plot(FF[,3],type='l')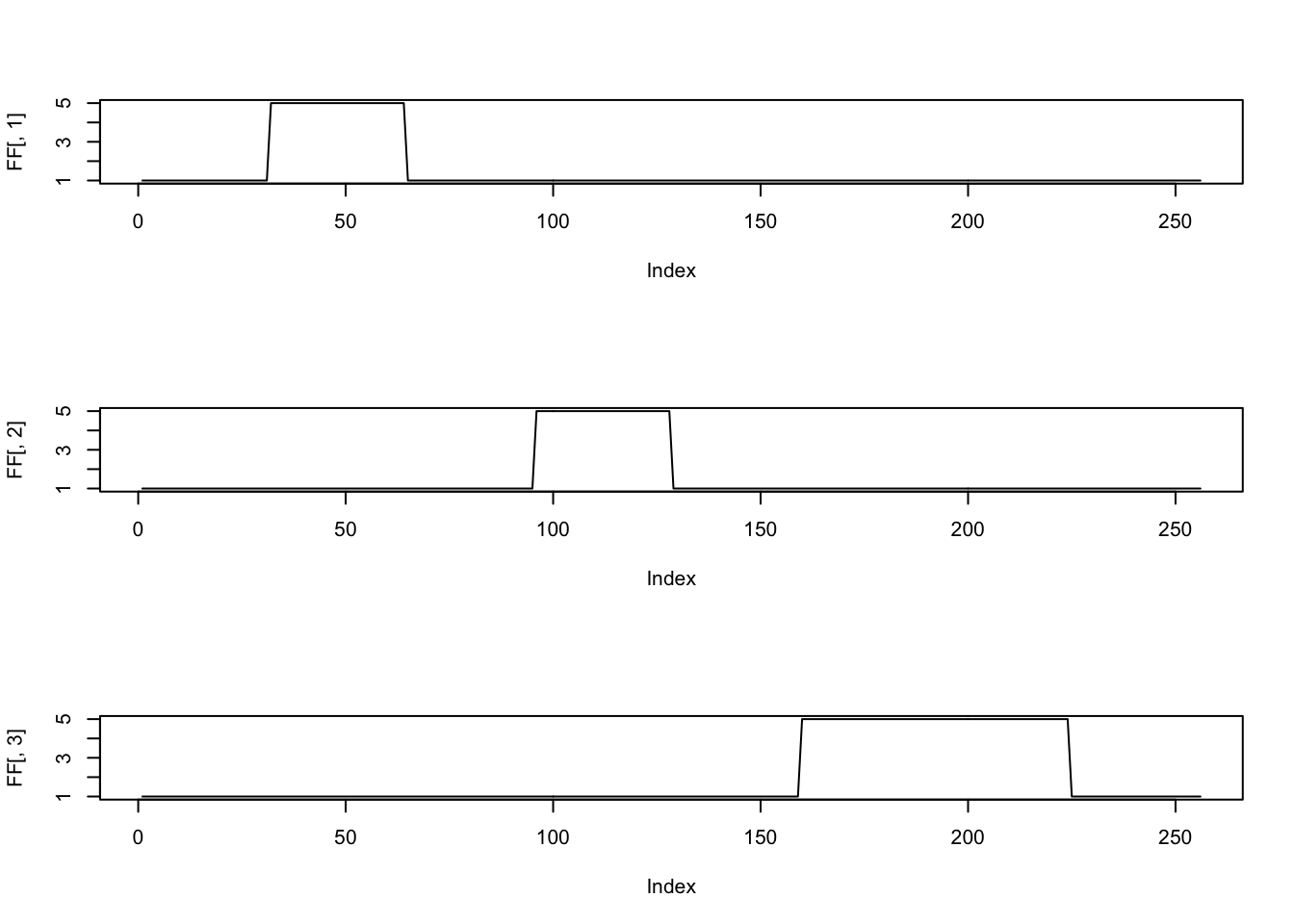
par(mfrow=c(3,1))
plot(FFF[,1],type='l')
abline(v=p,lty=2)
plot(FFF[,2],type='l')
abline(v=p,lty=2)
plot(FFF[,3],type='l')
abline(v=p,lty=2)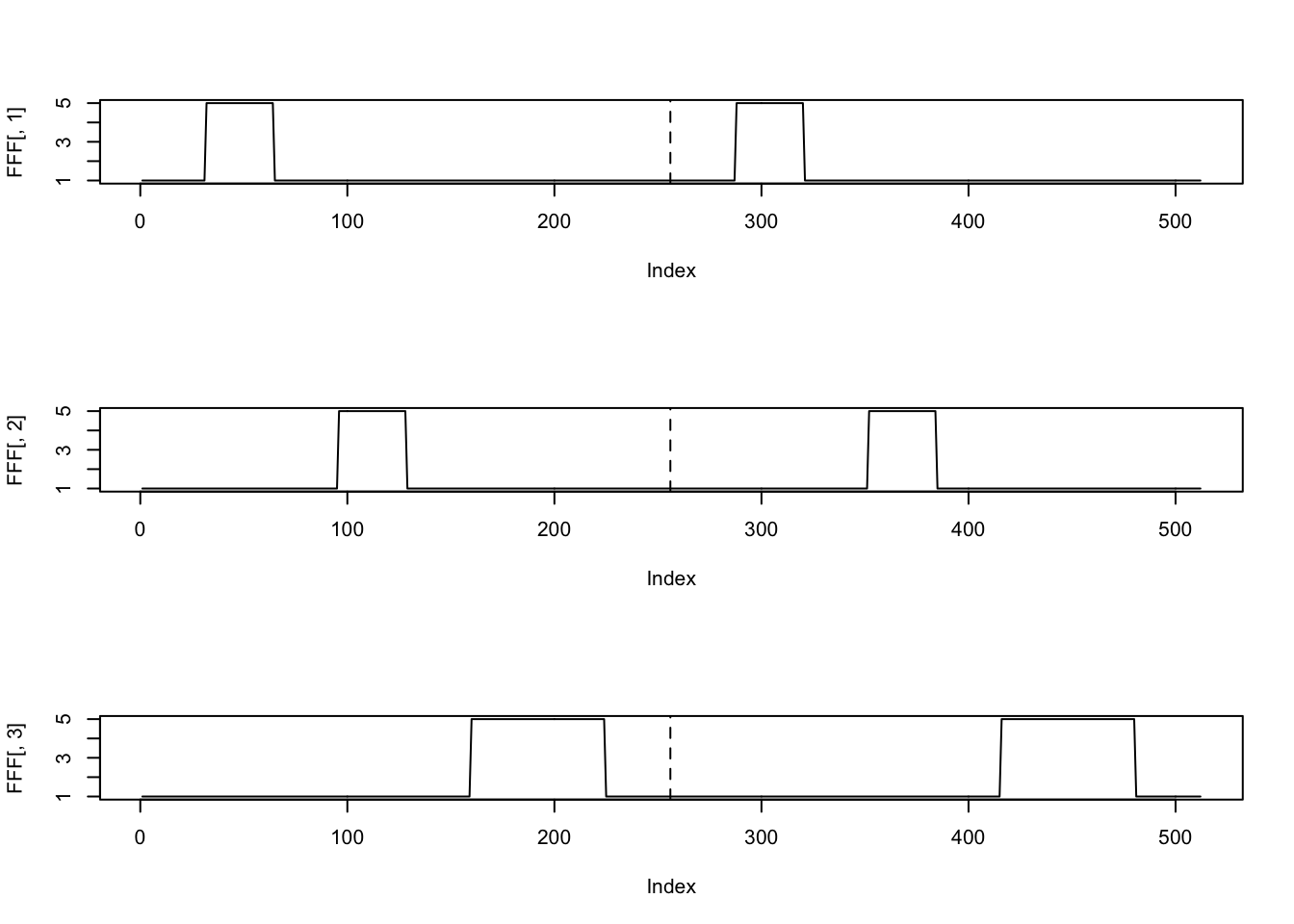
source('code/smooth_flash.R')Loading required package: usethisLoading flashr
Attaching package: 'testthat'The following object is masked from 'package:devtools':
test_fileLoading required package: MASSWaveThresh: R wavelet software, release 4.6.8, installedCopyright Guy Nason and others 1993-2016Note: nlevels has been renamed to nlevelsWT
Attaching package: 'wavethresh'The following object is masked from 'package:devtools':
wdsource('code/wave_ebmf.R')Loading flashrploter = function(EF,main){
par(mfrow=c(3,1))
for(k in 1:ncol(EF)){
plot(EF[,k],ylab=paste('f',k,sep=''),main=ifelse(k==1,main,""),type='l')
}
}ploter2 = function(EF,main){
p = nrow(EF)
par(mfrow=c(3,1))
for(k in 1:ncol(EF)){
plot(EF[,k],ylab=paste('f',k,sep=''),main=ifelse(k==1,main,""),type='l')
abline(v=p/2,lty=2)
}
}Let’s first take a look of single function case:
library(tictoc)
seed=12345
tic();fit.flash = flash(y[,1:p],var_type = 'by_row',seed = seed);toc()Fitting factor/loading 1 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -62031.23 Inf 2 -61963.63 6.76e+01 3 -61919.03 4.46e+01 4 -61892.79 2.62e+01 5 -61878.84 1.39e+01 6 -61871.85 6.99e+00 7 -61868.43 3.41e+00 8 -61866.78 1.65e+00 9 -61865.98 7.99e-01 10 -61865.60 3.86e-01 11 -61865.41 1.87e-01 12 -61865.32 9.06e-02 13 -61865.27 4.39e-02 14 -61865.25 2.13e-02 15 -61865.24 1.03e-02 16 -61865.24 5.02e-03Performing nullcheck... Deleting factor 1 decreases objective by 1.62e+04. Factor retained. Nullcheck complete. Objective: -61865.24Fitting factor/loading 2 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -45993.58 Inf 2 -45983.27 1.03e+01 3 -45980.13 3.14e+00 4 -45978.99 1.14e+00 5 -45978.58 4.09e-01 6 -45978.44 1.47e-01 7 -45978.38 5.31e-02 8 -45978.36 1.92e-02 9 -45978.36 6.91e-03Performing nullcheck... Deleting factor 2 decreases objective by 1.59e+04. Factor retained. Nullcheck complete. Objective: -45978.36Fitting factor/loading 3 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -28272.62 Inf 2 -28268.90 3.72e+00 3 -28268.89 5.75e-03Performing nullcheck... Deleting factor 3 decreases objective by 1.77e+04. Factor retained. Nullcheck complete. Objective: -28268.89Fitting factor/loading 4 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -28321.78 Inf 2 -28308.51 1.33e+01 3 -28306.89 1.62e+00 4 -28306.31 5.75e-01 5 -28305.98 3.37e-01 6 -28305.69 2.85e-01 7 -28305.38 3.12e-01 8 -28304.97 4.13e-01 9 -28303.90 1.07e+00 10 -28294.73 9.17e+00 11 -28294.42 3.17e-01 12 -28294.42 0.00e+00Performing nullcheck... Deleting factor 4 increases objective by 2.55e+01. Factor zeroed out. Nullcheck complete. Objective: -28268.890.725 sec elapsedtic();fit.dwt = wave_ebmf(y[,1:p]);toc()[1] "Fitting dimension 1"
[1] "Iteration 1 : obj -61233.381"
[1] "Iteration 2 : obj -61157.953"
[1] "Iteration 3 : obj -61109.053"
[1] "Iteration 4 : obj -61080.973"
[1] "Iteration 5 : obj -61066.273"
[1] "Iteration 6 : obj -61058.984"
[1] "Iteration 7 : obj -61055.466"
[1] "Iteration 8 : obj -61053.789"
[1] "Iteration 9 : obj -61052.994"
[1] "Iteration 10 : obj -61052.619"
[1] "Iteration 11 : obj -61052.442"
[1] "Iteration 12 : obj -61052.359"
[1] "Iteration 13 : obj -61052.32"
[1] "Iteration 14 : obj -61052.301"
[1] "Iteration 15 : obj -61052.293"
[1] "Performing nullcheck"
[1] "Deleting factor 1 decreases objective by 17049.363"
[1] "Fitting dimension 2"
[1] "Iteration 1 : obj -44225.684"
[1] "Iteration 2 : obj -44215.094"
[1] "Iteration 3 : obj -44211.735"
[1] "Iteration 4 : obj -44210.574"
[1] "Iteration 5 : obj -44210.174"
[1] "Iteration 6 : obj -44210.036"
[1] "Iteration 7 : obj -44209.989"
[1] "Iteration 8 : obj -44209.972"
[1] "Iteration 9 : obj -44209.966"
[1] "Performing nullcheck"
[1] "Deleting factor 2 decreases objective by 16842.324"
[1] "Fitting dimension 3"
[1] "Iteration 1 : obj -25394.505"
[1] "Iteration 2 : obj -25391.799"
[1] "Iteration 3 : obj -25391.799"
[1] "Performing nullcheck"
[1] "Deleting factor 3 decreases objective by 18818.167"
[1] "Fitting dimension 4"
[1] "Iteration 1 : obj -25455.565"
[1] "Iteration 2 : obj -25435.391"
[1] "Iteration 3 : obj -25425.674"
[1] "Iteration 4 : obj -25413.52"
[1] "Iteration 5 : obj -25392.367"
[1] "factor zeroed out"
[1] "Performing nullcheck"
[1] "Deleting factor 4 increases objective by 0.568"1.235 sec elapsedploter(fit.flash$ldf$f,main='flash')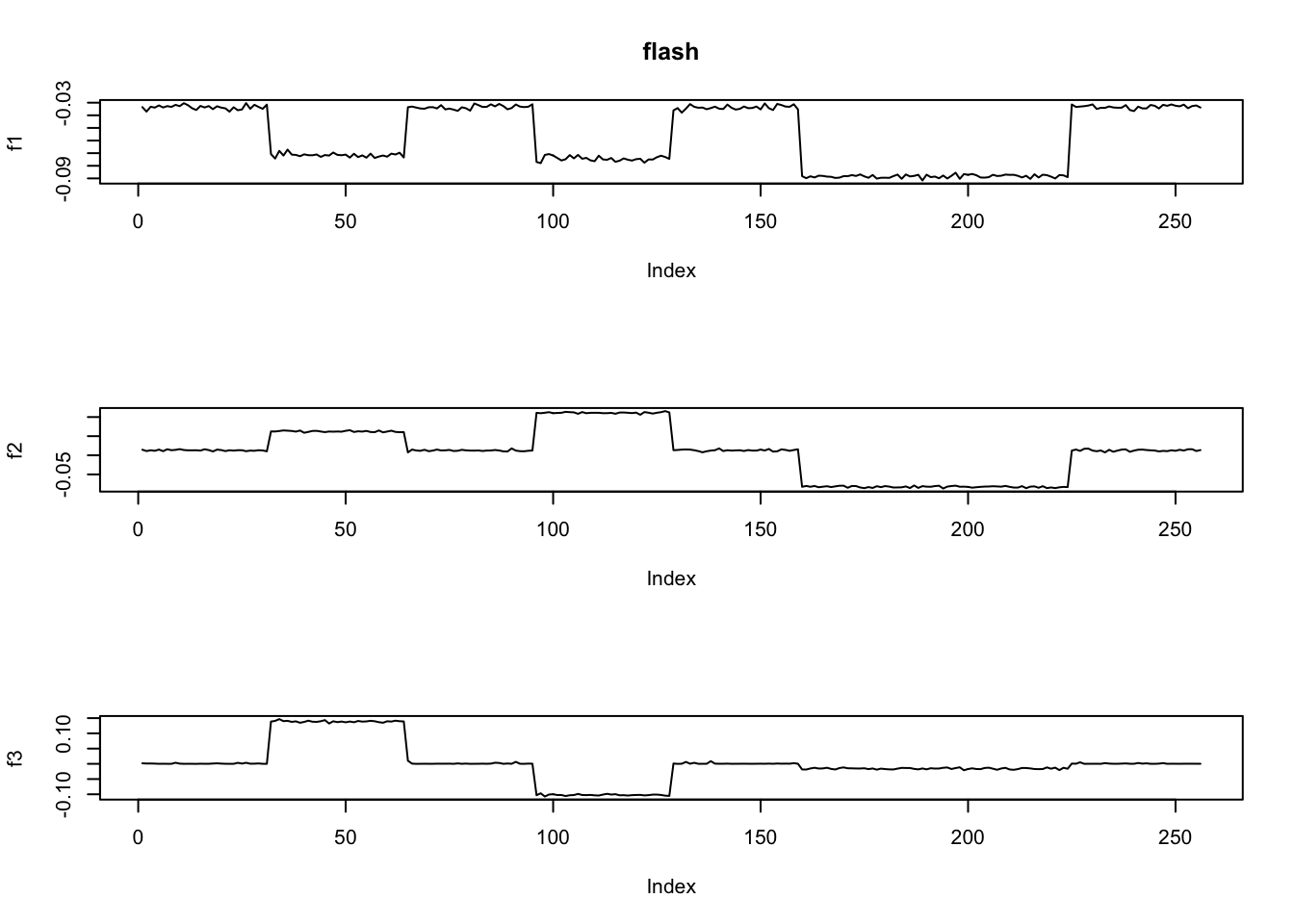
ploter(fit.dwt$ldf$f,main='wave_flash')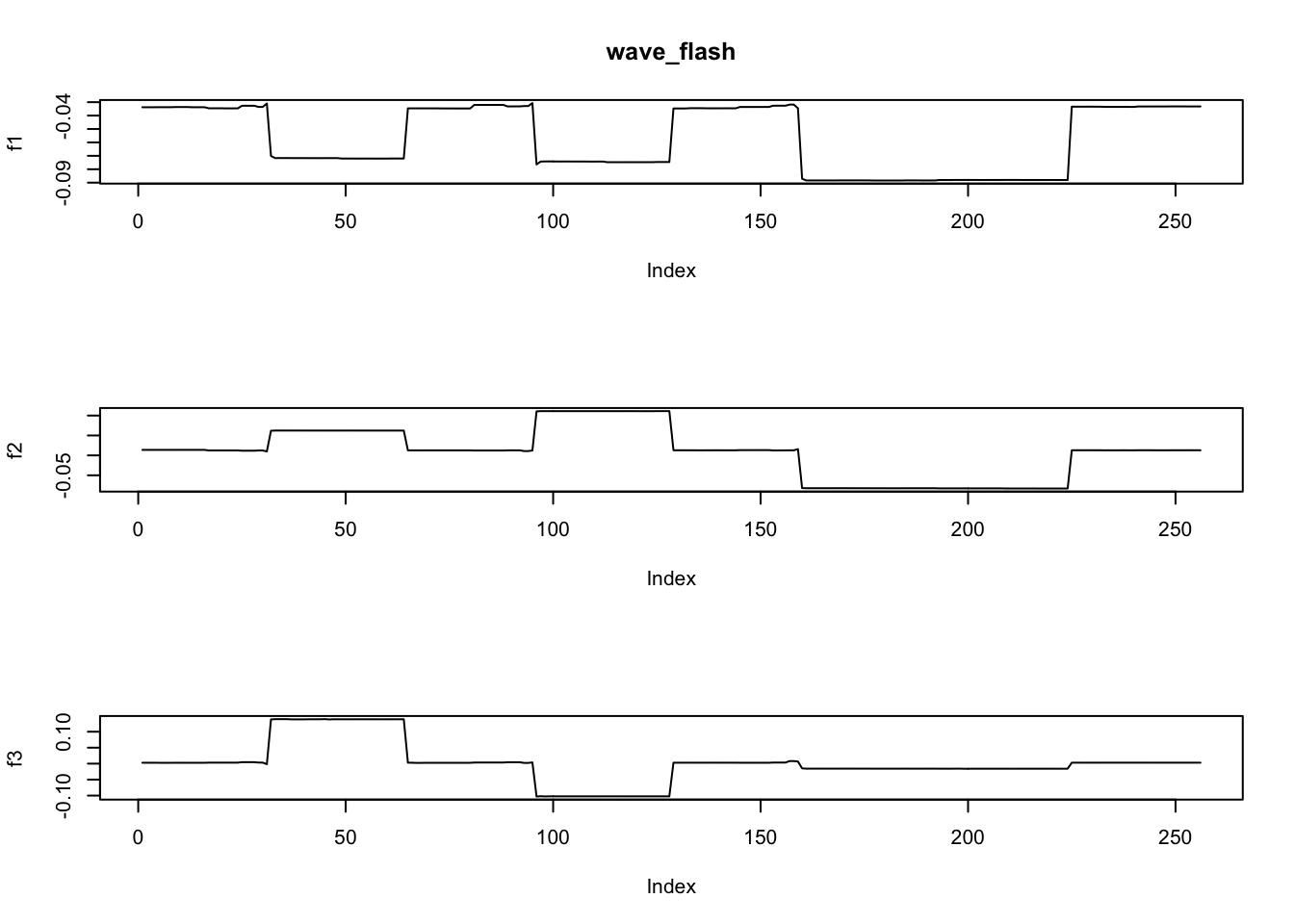
Try to use different initialization
fit.dwt = wave_ebmf(y[,1:p],init_fn = 'udv_svd')[1] "Fitting dimension 1"
[1] "Iteration 1 : obj -61229.797"
[1] "Iteration 2 : obj -61155.398"
[1] "Iteration 3 : obj -61107.483"
[1] "Iteration 4 : obj -61080.114"
[1] "Iteration 5 : obj -61065.836"
[1] "Iteration 6 : obj -61058.77"
[1] "Iteration 7 : obj -61055.363"
[1] "Iteration 8 : obj -61053.74"
[1] "Iteration 9 : obj -61052.971"
[1] "Iteration 10 : obj -61052.608"
[1] "Iteration 11 : obj -61052.437"
[1] "Iteration 12 : obj -61052.356"
[1] "Iteration 13 : obj -61052.319"
[1] "Iteration 14 : obj -61052.301"
[1] "Iteration 15 : obj -61052.292"
[1] "Performing nullcheck"
[1] "Deleting factor 1 decreases objective by 17049.363"
[1] "Fitting dimension 2"
[1] "Iteration 1 : obj -44227.663"
[1] "Iteration 2 : obj -44215.804"
[1] "Iteration 3 : obj -44211.979"
[1] "Iteration 4 : obj -44210.657"
[1] "Iteration 5 : obj -44210.201"
[1] "Iteration 6 : obj -44210.044"
[1] "Iteration 7 : obj -44209.99"
[1] "Iteration 8 : obj -44209.971"
[1] "Iteration 9 : obj -44209.964"
[1] "Performing nullcheck"
[1] "Deleting factor 2 decreases objective by 16842.326"
[1] "Fitting dimension 3"
[1] "Iteration 1 : obj -25394.506"
[1] "Iteration 2 : obj -25391.8"
[1] "Iteration 3 : obj -25391.8"
[1] "Performing nullcheck"
[1] "Deleting factor 3 decreases objective by 18818.164"
[1] "Fitting dimension 4"
[1] "Iteration 1 : obj -25455.85"
[1] "Iteration 2 : obj -25435.637"
[1] "Iteration 3 : obj -25425.166"
[1] "Iteration 4 : obj -25412.613"
[1] "Iteration 5 : obj -25392.242"
[1] "factor zeroed out"
[1] "Performing nullcheck"
[1] "Deleting factor 4 increases objective by 0.443"ploter(fit.dwt$ldf$f,main='wave_flash, svd init')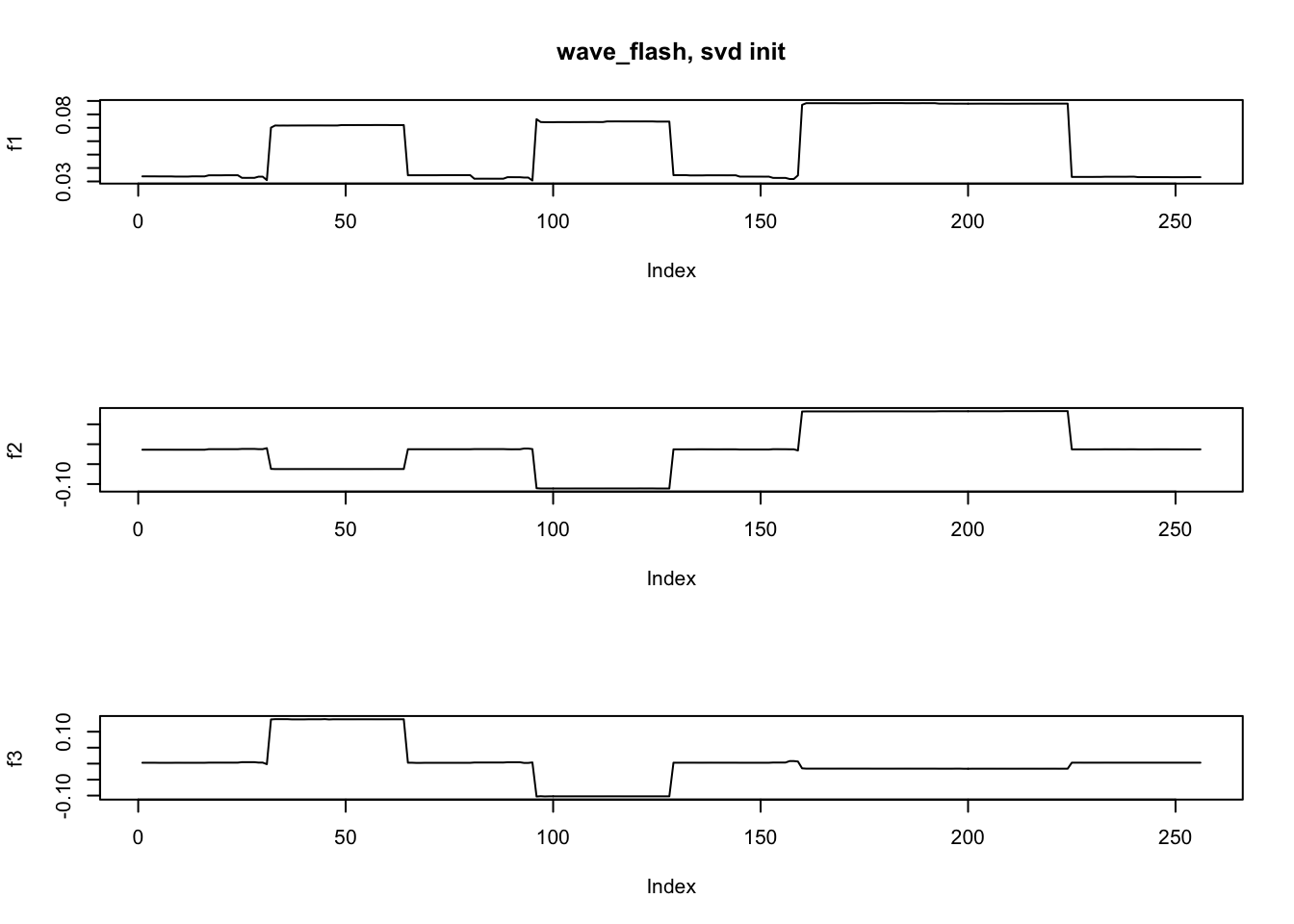
Modify \(L\) so that there columns are independent
set.seed(123)
L = cbind(c(rep(1,n/3),rep(0,n/3*2)),
c(rep(0,n/3),rep(-1,n/3),rep(0,n/3)),
c(rep(0,n/3*2),rep(1,n/3)))
s = 0.5
y = tcrossprod(L,FFF) + matrix(rnorm(n*p*2,0,s),nrow=n,ncol=p*2)seed=12345
tic();fit.flash = flash(y[,1:p],var_type = 'by_row',seed = seed);toc()Fitting factor/loading 1 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -54425.89 Inf 2 -53605.18 8.21e+02 3 -52008.60 1.60e+03 4 -50504.65 1.50e+03 5 -50181.38 3.23e+02 6 -50167.70 1.37e+01 7 -50167.39 3.14e-01 8 -50167.38 6.69e-03Performing nullcheck... Deleting factor 1 decreases objective by 1.86e+04. Factor retained. Nullcheck complete. Objective: -50167.38Fitting factor/loading 2 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -41470.93 Inf 2 -41468.27 2.66e+00 3 -41463.14 5.13e+00 4 -41441.62 2.15e+01 5 -41352.66 8.90e+01 6 -41008.11 3.45e+02 7 -39954.08 1.05e+03 8 -38328.48 1.63e+03 9 -37744.72 5.84e+02 10 -37715.68 2.90e+01 11 -37715.12 5.61e-01 12 -37715.11 1.04e-02 13 -37715.11 1.98e-04Performing nullcheck... Deleting factor 2 decreases objective by 1.25e+04. Factor retained. Nullcheck complete. Objective: -37715.11Fitting factor/loading 3 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -26563.99 Inf 2 -26561.36 2.63e+00 3 -26561.36 1.98e-03Performing nullcheck... Deleting factor 3 decreases objective by 1.12e+04. Factor retained. Nullcheck complete. Objective: -26561.36Fitting factor/loading 4 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -26624.61 Inf 2 -26607.88 1.67e+01 3 -26602.79 5.09e+00 4 -26585.60 1.72e+01 5 -26585.21 3.93e-01 6 -26585.21 0.00e+00Performing nullcheck... Deleting factor 4 increases objective by 2.38e+01. Factor zeroed out. Nullcheck complete. Objective: -26561.360.411 sec elapsedtic();fit.dwt = wave_ebmf(y[,1:p]);toc()[1] "Fitting dimension 1"
[1] "Iteration 1 : obj -53709.449"
[1] "Iteration 2 : obj -52827.44"
[1] "Iteration 3 : obj -51099.92"
[1] "Iteration 4 : obj -49587.504"
[1] "Iteration 5 : obj -49332.826"
[1] "Iteration 6 : obj -49325.191"
[1] "Iteration 7 : obj -49325.056"
[1] "Iteration 8 : obj -49325.053"
[1] "Performing nullcheck"
[1] "Deleting factor 1 decreases objective by 19426.972"
[1] "Fitting dimension 2"
[1] "Iteration 1 : obj -40002.025"
[1] "Iteration 2 : obj -40001.487"
[1] "Iteration 3 : obj -40001.37"
[1] "Iteration 4 : obj -40001.129"
[1] "Iteration 5 : obj -39999.652"
[1] "Iteration 6 : obj -39991.509"
[1] "Iteration 7 : obj -39952.018"
[1] "Iteration 8 : obj -39784.233"
[1] "Iteration 9 : obj -39163.125"
[1] "Iteration 10 : obj -37629.75"
[1] "Iteration 11 : obj -36311.309"
[1] "Iteration 12 : obj -36152.674"
[1] "Iteration 13 : obj -36148.577"
[1] "Iteration 14 : obj -36148.52"
[1] "Iteration 15 : obj -36148.52"
[1] "Performing nullcheck"
[1] "Deleting factor 2 decreases objective by 13176.534"
[1] "Fitting dimension 3"
[1] "Iteration 1 : obj -24283.569"
[1] "Iteration 2 : obj -24281.024"
[1] "Iteration 3 : obj -24281.023"
[1] "Performing nullcheck"
[1] "Deleting factor 3 decreases objective by 11867.497"
[1] "Fitting dimension 4"
[1] "Iteration 1 : obj -24340.149"
[1] "Iteration 2 : obj -24323.602"
[1] "Iteration 3 : obj -24318.697"
[1] "Iteration 4 : obj -24312.346"
[1] "Iteration 5 : obj -24296.374"
[1] "loading zeroed out"
[1] "Performing nullcheck"
[1] "Deleting factor 4 increases objective by 1.587"0.994 sec elapsedploter(fit.flash$ldf$f,main='flash')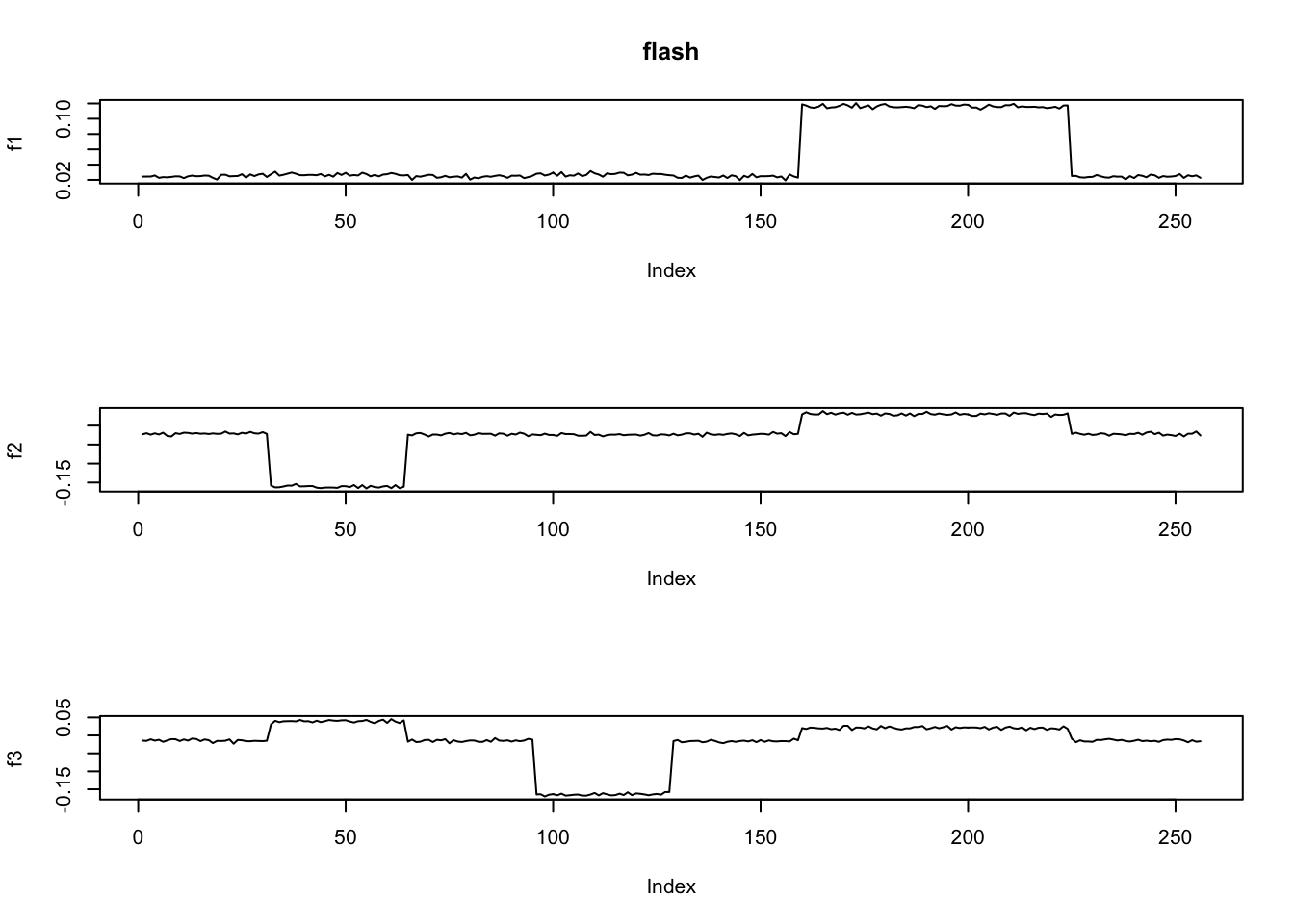
ploter(fit.dwt$ldf$f,main='wave_flash')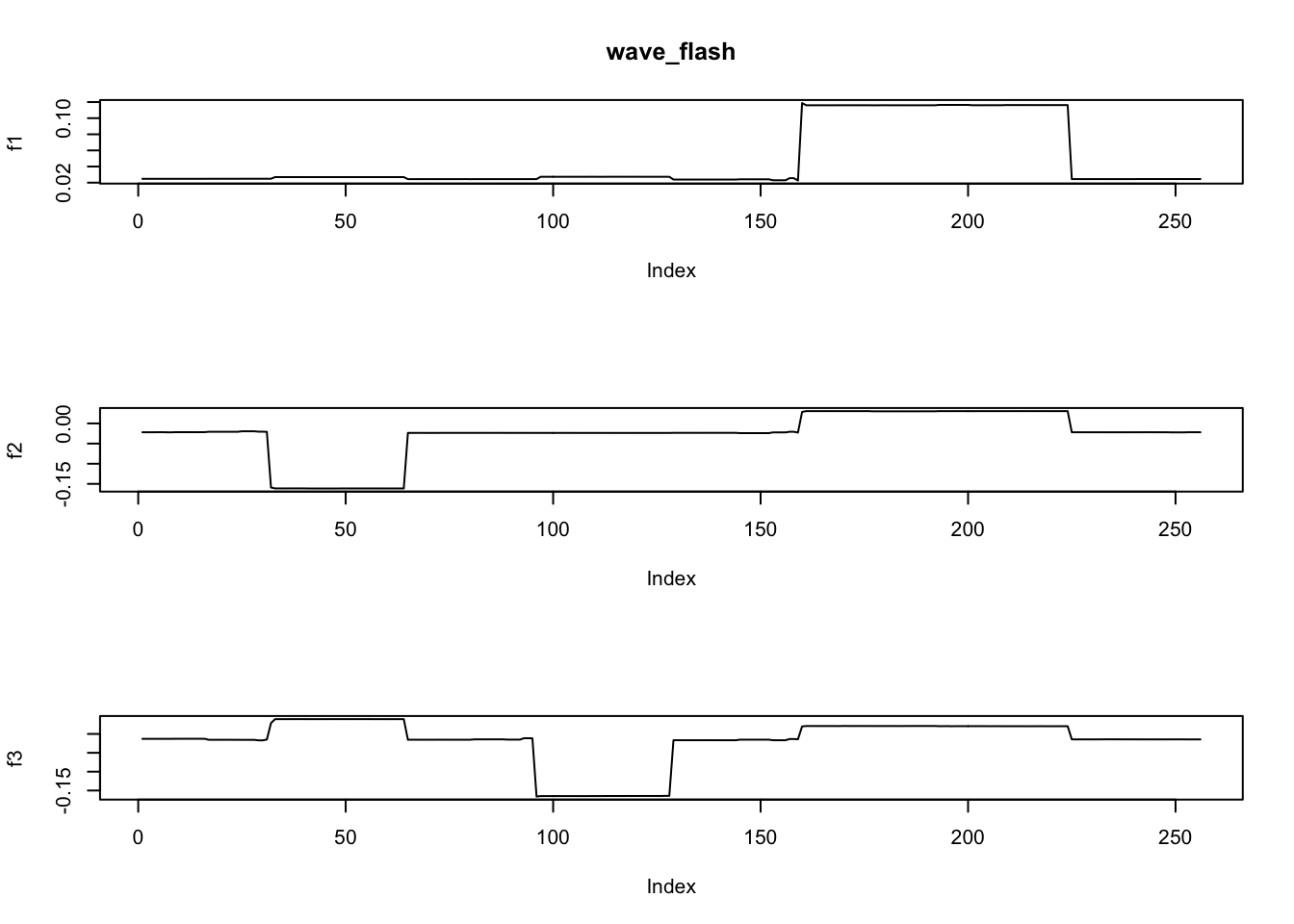
Two functions
seed=12345
tic();fit.flash = flash(y,var_type = 'by_row',seed = seed);toc()Fitting factor/loading 1 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -108732.64 Inf 2 -107198.23 1.53e+03 3 -104120.27 3.08e+03 4 -101003.79 3.12e+03 5 -100257.86 7.46e+02 6 -100224.90 3.30e+01 7 -100224.18 7.19e-01 8 -100224.17 1.43e-02 9 -100224.17 2.80e-04Performing nullcheck... Deleting factor 1 decreases objective by 3.74e+04. Factor retained. Nullcheck complete. Objective: -100224.17Fitting factor/loading 2 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -82205.78 Inf 2 -82199.57 6.21e+00 3 -82182.47 1.71e+01 4 -82111.09 7.14e+01 5 -81820.53 2.91e+02 6 -80751.70 1.07e+03 7 -77976.59 2.78e+03 8 -75108.95 2.87e+03 9 -74590.44 5.19e+02 10 -74575.60 1.48e+01 11 -74575.35 2.54e-01 12 -74575.34 4.44e-03Performing nullcheck... Deleting factor 2 decreases objective by 2.56e+04. Factor retained. Nullcheck complete. Objective: -74575.34Fitting factor/loading 3 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -51738.85 Inf 2 -51734.74 4.11e+00 3 -51734.73 2.77e-03Performing nullcheck... Deleting factor 3 decreases objective by 2.28e+04. Factor retained. Nullcheck complete. Objective: -51734.73Fitting factor/loading 4 (stop when difference in obj. is < 1.00e-02): Iteration Objective Obj Diff 1 -51815.30 Inf 2 -51792.18 2.31e+01 3 -51788.56 3.63e+00 4 -51785.80 2.76e+00 5 -51777.15 8.65e+00 6 -51736.39 4.08e+01 7 -51736.39 2.69e-04Performing nullcheck... Deleting factor 4 increases objective by 1.66e+00. Factor zeroed out. Nullcheck complete. Objective: -51734.730.602 sec elapsedtic();fit.dwt = wave_ebmf(y);toc()[1] "Fitting dimension 1"
[1] "Iteration 1 : obj -107292.443"
[1] "Iteration 2 : obj -105642.273"
[1] "Iteration 3 : obj -102305.493"
[1] "Iteration 4 : obj -99150.002"
[1] "Iteration 5 : obj -98554.208"
[1] "Iteration 6 : obj -98535.653"
[1] "Iteration 7 : obj -98535.338"
[1] "Iteration 8 : obj -98535.333"
[1] "Performing nullcheck"
[1] "Deleting factor 1 decreases objective by 39091.254"
[1] "Fitting dimension 2"
[1] "Iteration 1 : obj -79256.738"
[1] "Iteration 2 : obj -79255.162"
[1] "Iteration 3 : obj -79250.46"
[1] "Iteration 4 : obj -79228.677"
[1] "Iteration 5 : obj -79130.16"
[1] "Iteration 6 : obj -78715.988"
[1] "Iteration 7 : obj -77232.717"
[1] "Iteration 8 : obj -73908.739"
[1] "Iteration 9 : obj -71625.121"
[1] "Iteration 10 : obj -71430.346"
[1] "Iteration 11 : obj -71426.573"
[1] "Iteration 12 : obj -71426.51"
[1] "Iteration 13 : obj -71426.51"
[1] "Performing nullcheck"
[1] "Deleting factor 2 decreases objective by 27108.823"
[1] "Fitting dimension 3"
[1] "Iteration 1 : obj -47174.395"
[1] "Iteration 2 : obj -47170.479"
[1] "Iteration 3 : obj -47170.478"
[1] "Performing nullcheck"
[1] "Deleting factor 3 decreases objective by 24256.032"
[1] "Fitting dimension 4"
[1] "Iteration 1 : obj -47241.861"
[1] "Iteration 2 : obj -47218.33"
[1] "Iteration 3 : obj -47213.905"
[1] "Iteration 4 : obj -47210.322"
[1] "Iteration 5 : obj -47205.739"
[1] "Iteration 6 : obj -47201.604"
[1] "Iteration 7 : obj -47197.79"
[1] "Iteration 8 : obj -47194.883"
[1] "Iteration 9 : obj -47193.295"
[1] "Iteration 10 : obj -47192.457"
[1] "Iteration 11 : obj -47191.904"
[1] "Iteration 12 : obj -47191.472"
[1] "Iteration 13 : obj -47191.123"
[1] "Iteration 14 : obj -47190.807"
[1] "Iteration 15 : obj -47190.461"
[1] "Iteration 16 : obj -47190.064"
[1] "Iteration 17 : obj -47189.744"
[1] "Iteration 18 : obj -47189.485"
[1] "Iteration 19 : obj -47189.279"
[1] "Iteration 20 : obj -47189.114"
[1] "Iteration 21 : obj -47188.982"
[1] "Iteration 22 : obj -47188.876"
[1] "Iteration 23 : obj -47188.792"
[1] "Iteration 24 : obj -47188.727"
[1] "Iteration 25 : obj -47188.676"
[1] "Iteration 26 : obj -47188.634"
[1] "Iteration 27 : obj -47188.596"
[1] "Iteration 28 : obj -47188.559"
[1] "Iteration 29 : obj -47188.519"
[1] "Iteration 30 : obj -47188.47"
[1] "Iteration 31 : obj -47188.402"
[1] "Iteration 32 : obj -47188.29"
[1] "Iteration 33 : obj -47205.281"
[1] "An iteration decreased the objective"
[1] "Performing nullcheck"
[1] "Deleting factor 4 increases objective by 34.803"3.053 sec elapsedploter2(fit.flash$ldf$f,main='flash')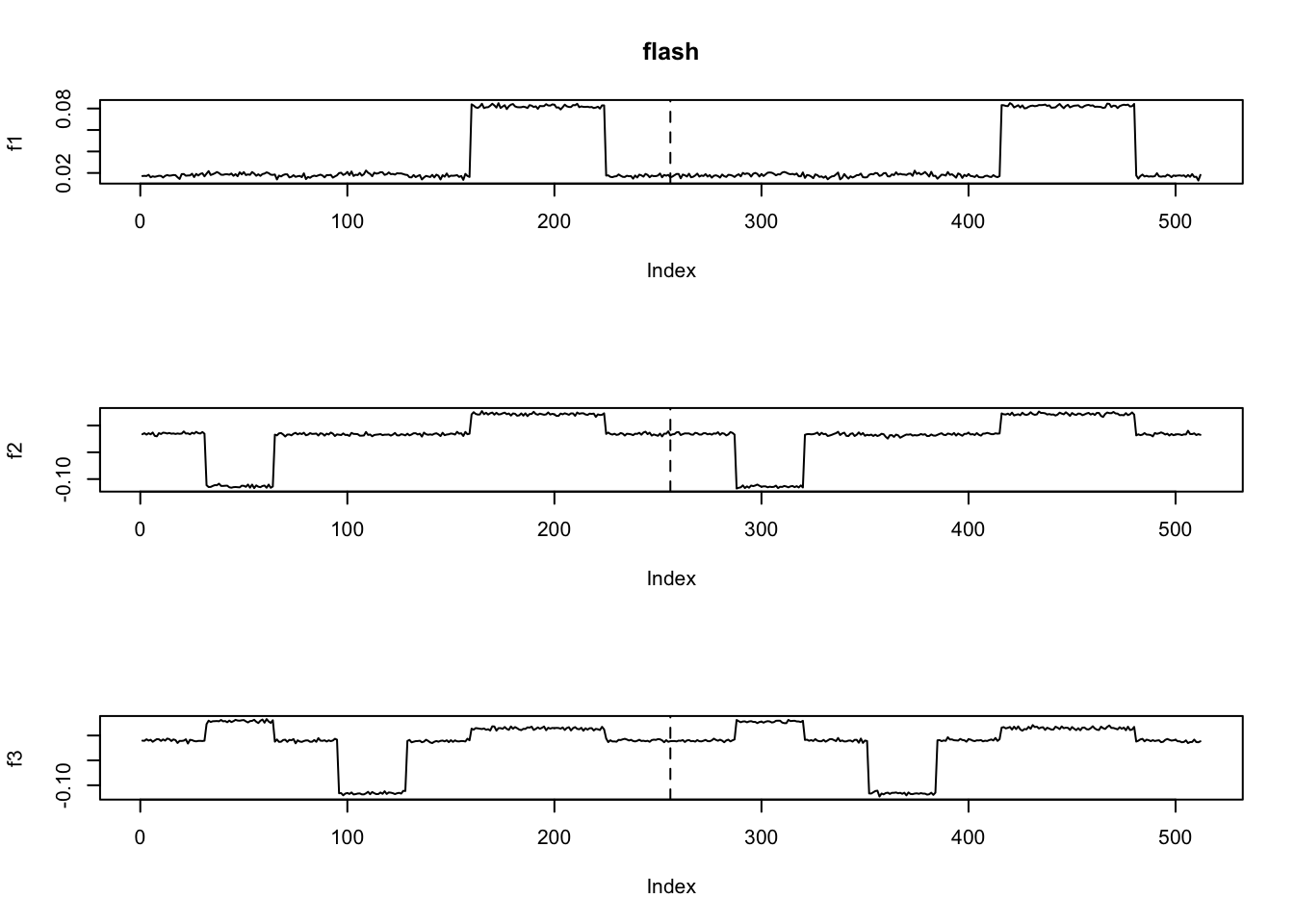
ploter2(fit.dwt$ldf$f,main='wave_flash')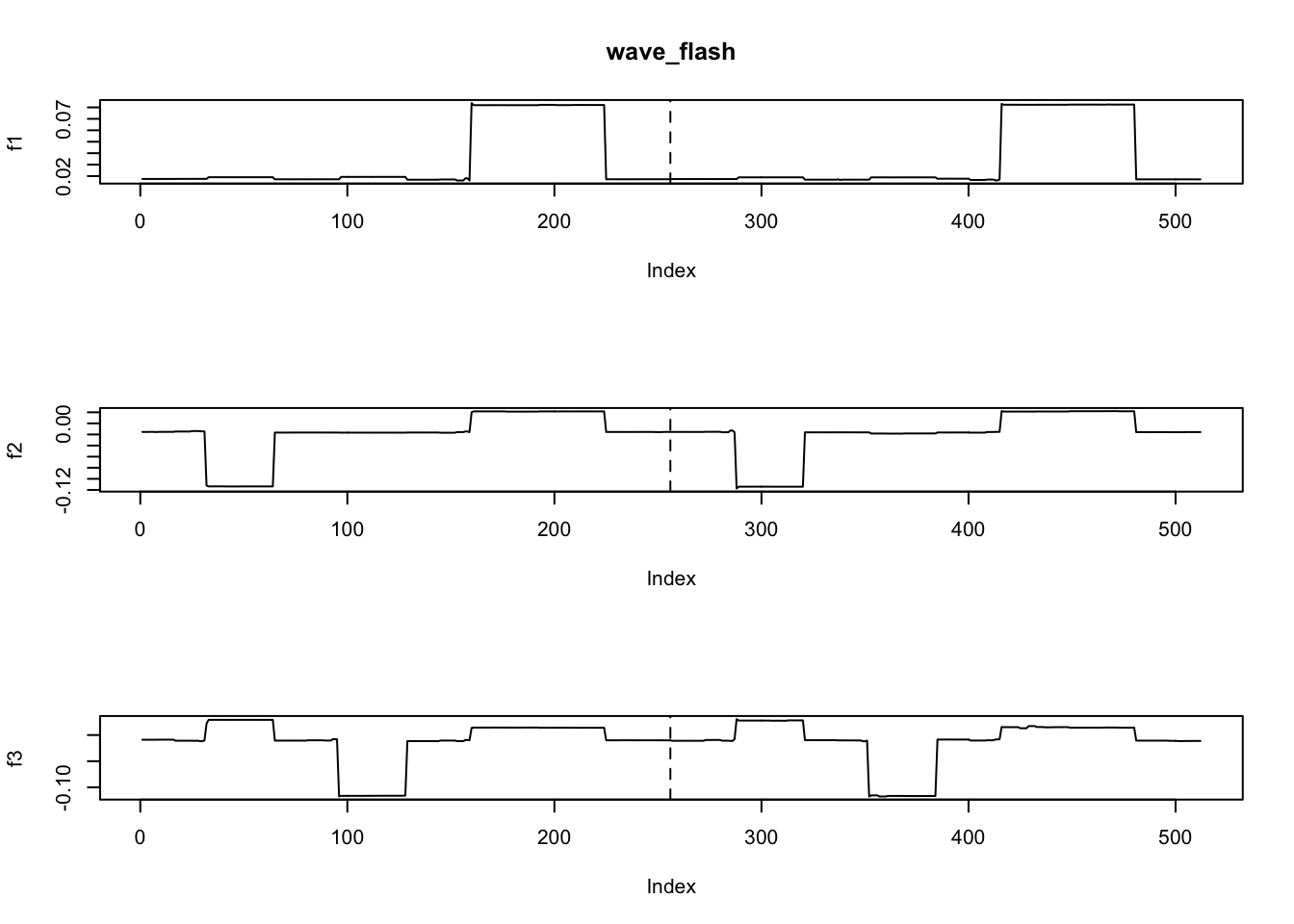
Poisson case
ploter3 = function(EF,main){
p = nrow(EF)
par(mfrow=c(3,1))
for(k in 1:ncol(EF)){
plot(EF[,k],ylab=paste('f',k,sep=''),main=ifelse(k==1,main,""),type='l')
abline(v=p/2,lty=2)
}
}Start with a single function case:
library(stm)
set.seed(123)
n = 120
p = 256
K= 3
FF = matrix(1, nrow=p, ncol=K)
FF[(p/8*1):(p/8*2),1] = 5
FF[(p/8*3):(p/8*4),2] = 5
FF[(p/8*5):(p/8*7),3] = 5
L = matrix(rgamma(n*K,2),ncol=K)
y = matrix(rpois(n*p,tcrossprod(L,FF)),nrow=n)
fit.nmf = NNLM::nnmf(y,k=3,method = 'scd',loss='mkl')
ploter(t(fit.nmf$H),main='nmf,scd=mkl')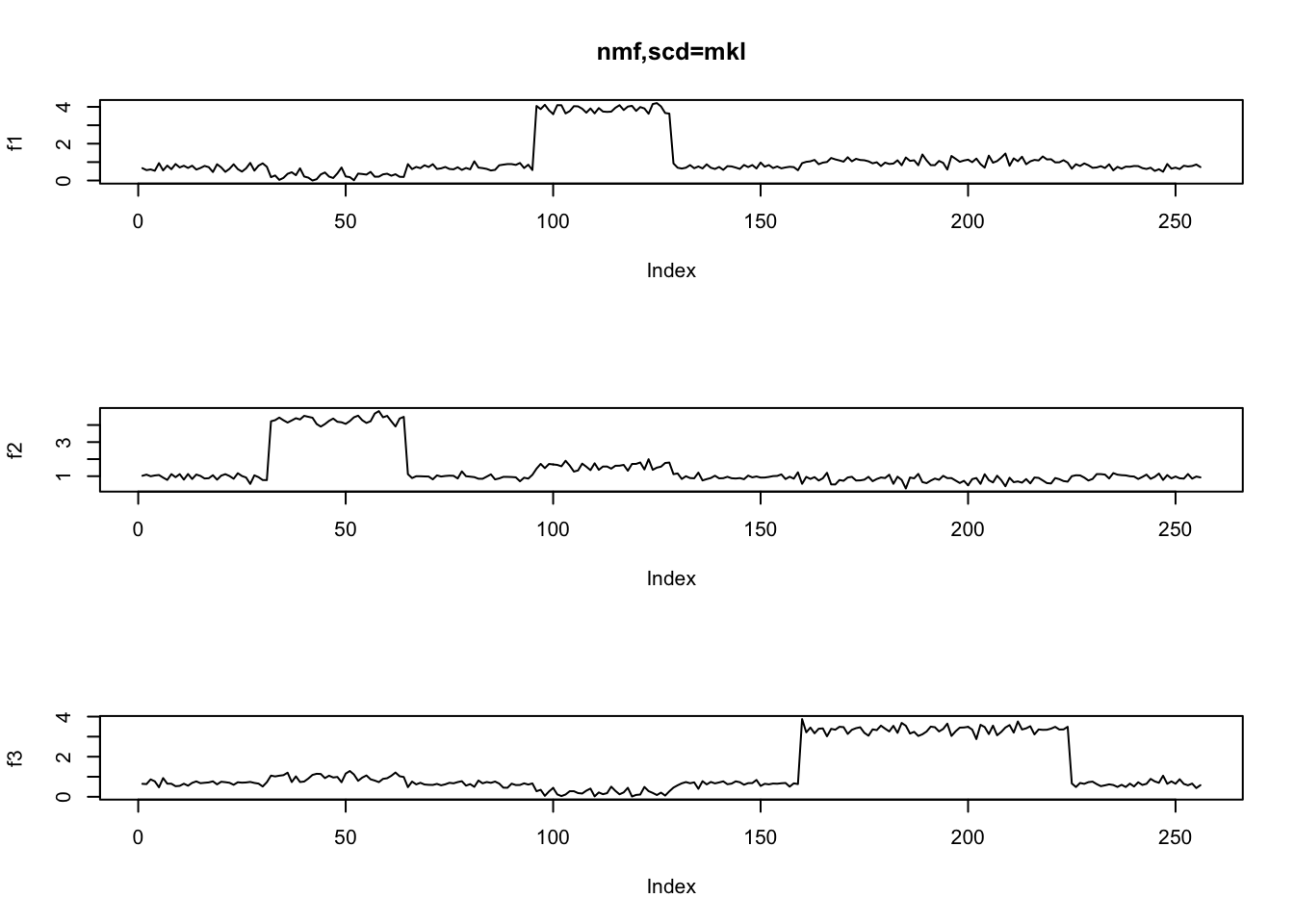
fit.gom = cluster.mix(y,smooth = FALSE,K=3,tol=1e-3,maxit = 100)[1] "iteration"
[1] 1
[1] "phi difference"
[1] 3988.362
[1] "pi difference"
[1] 0.2680048
[1] "negative loglikelihood"
[1] 1556268
[1] "iteration"
[1] 2
[1] "phi difference"
[1] 0.007248152
[1] "pi difference"
[1] 0.01655635
[1] "negative loglikelihood"
[1] 1556132
[1] "iteration"
[1] 3
[1] "phi difference"
[1] 0.01425026
[1] "pi difference"
[1] 0.0169203
[1] "negative loglikelihood"
[1] 1555973
[1] "iteration"
[1] 4
[1] "phi difference"
[1] 0.02125566
[1] "pi difference"
[1] 0.01778377
[1] "negative loglikelihood"
[1] 1555773
[1] "iteration"
[1] 5
[1] "phi difference"
[1] 0.02832821
[1] "pi difference"
[1] 0.01903516
[1] "negative loglikelihood"
[1] 1555517
[1] "iteration"
[1] 6
[1] "phi difference"
[1] 0.03540202
[1] "pi difference"
[1] 0.0205576
[1] "negative loglikelihood"
[1] 1555191
[1] "iteration"
[1] 7
[1] "phi difference"
[1] 0.04222619
[1] "pi difference"
[1] 0.02222088
[1] "negative loglikelihood"
[1] 1554784
[1] "iteration"
[1] 8
[1] "phi difference"
[1] 0.04834576
[1] "pi difference"
[1] 0.02378133
[1] "negative loglikelihood"
[1] 1554296
[1] "iteration"
[1] 9
[1] "phi difference"
[1] 0.05218435
[1] "pi difference"
[1] 0.0249727
[1] "negative loglikelihood"
[1] 1553741
[1] "iteration"
[1] 10
[1] "phi difference"
[1] 0.05384307
[1] "pi difference"
[1] 0.02565832
[1] "negative loglikelihood"
[1] 1553150
[1] "iteration"
[1] 11
[1] "phi difference"
[1] 0.05318603
[1] "pi difference"
[1] 0.02564275
[1] "negative loglikelihood"
[1] 1552564
[1] "iteration"
[1] 12
[1] "phi difference"
[1] 0.04992299
[1] "pi difference"
[1] 0.02484726
[1] "negative loglikelihood"
[1] 1552023
[1] "iteration"
[1] 13
[1] "phi difference"
[1] 0.04313862
[1] "pi difference"
[1] 0.02360919
[1] "negative loglikelihood"
[1] 1551555
[1] "iteration"
[1] 14
[1] "phi difference"
[1] 0.0350059
[1] "pi difference"
[1] 0.02240167
[1] "negative loglikelihood"
[1] 1551167
[1] "iteration"
[1] 15
[1] "phi difference"
[1] 0.02670056
[1] "pi difference"
[1] 0.02130135
[1] "negative loglikelihood"
[1] 1550849
[1] "iteration"
[1] 16
[1] "phi difference"
[1] 0.01867192
[1] "pi difference"
[1] 0.02026996
[1] "negative loglikelihood"
[1] 1550581
[1] "iteration"
[1] 17
[1] "phi difference"
[1] 0.01195962
[1] "pi difference"
[1] 0.01964568
[1] "negative loglikelihood"
[1] 1550344
[1] "iteration"
[1] 18
[1] "phi difference"
[1] 0.007249337
[1] "pi difference"
[1] 0.01917317
[1] "negative loglikelihood"
[1] 1550121
[1] "iteration"
[1] 19
[1] "phi difference"
[1] 0.007401366
[1] "pi difference"
[1] 0.01882432
[1] "negative loglikelihood"
[1] 1549901
[1] "iteration"
[1] 20
[1] "phi difference"
[1] 0.007840253
[1] "pi difference"
[1] 0.01859933
[1] "negative loglikelihood"
[1] 1549681
[1] "iteration"
[1] 21
[1] "phi difference"
[1] 0.00795566
[1] "pi difference"
[1] 0.01837616
[1] "negative loglikelihood"
[1] 1549459
[1] "iteration"
[1] 22
[1] "phi difference"
[1] 0.008185762
[1] "pi difference"
[1] 0.01812838
[1] "negative loglikelihood"
[1] 1549239
[1] "iteration"
[1] 23
[1] "phi difference"
[1] 0.008556548
[1] "pi difference"
[1] 0.01773103
[1] "negative loglikelihood"
[1] 1549027
[1] "iteration"
[1] 24
[1] "phi difference"
[1] 0.008651467
[1] "pi difference"
[1] 0.01713919
[1] "negative loglikelihood"
[1] 1548829
[1] "iteration"
[1] 25
[1] "phi difference"
[1] 0.008499844
[1] "pi difference"
[1] 0.01630018
[1] "negative loglikelihood"
[1] 1548648
[1] "iteration"
[1] 26
[1] "phi difference"
[1] 0.008148614
[1] "pi difference"
[1] 0.01523472
[1] "negative loglikelihood"
[1] 1548490
[1] "iteration"
[1] 27
[1] "phi difference"
[1] 0.007721917
[1] "pi difference"
[1] 0.01397762
[1] "negative loglikelihood"
[1] 1548354
[1] "iteration"
[1] 28
[1] "phi difference"
[1] 0.007359908
[1] "pi difference"
[1] 0.01258646
[1] "negative loglikelihood"
[1] 1548242
[1] "iteration"
[1] 29
[1] "phi difference"
[1] 0.006932472
[1] "pi difference"
[1] 0.01134788
[1] "negative loglikelihood"
[1] 1548149
[1] "iteration"
[1] 30
[1] "phi difference"
[1] 0.006280522
[1] "pi difference"
[1] 0.01030838
[1] "negative loglikelihood"
[1] 1548075
[1] "iteration"
[1] 31
[1] "phi difference"
[1] 0.005759753
[1] "pi difference"
[1] 0.009294335
[1] "negative loglikelihood"
[1] 1548016
[1] "iteration"
[1] 32
[1] "phi difference"
[1] 0.005267121
[1] "pi difference"
[1] 0.008331438
[1] "negative loglikelihood"
[1] 1547969
[1] "iteration"
[1] 33
[1] "phi difference"
[1] 0.004801244
[1] "pi difference"
[1] 0.007503247
[1] "negative loglikelihood"
[1] 1547931
[1] "iteration"
[1] 34
[1] "phi difference"
[1] 0.004377284
[1] "pi difference"
[1] 0.006784135
[1] "negative loglikelihood"
[1] 1547901
[1] "iteration"
[1] 35
[1] "phi difference"
[1] 0.003960138
[1] "pi difference"
[1] 0.006223292
[1] "negative loglikelihood"
[1] 1547876
[1] "iteration"
[1] 36
[1] "phi difference"
[1] 0.003445544
[1] "pi difference"
[1] 0.005720539
[1] "negative loglikelihood"
[1] 1547856
[1] "iteration"
[1] 37
[1] "phi difference"
[1] 0.002969403
[1] "pi difference"
[1] 0.005232668
[1] "negative loglikelihood"
[1] 1547840
[1] "iteration"
[1] 38
[1] "phi difference"
[1] 0.002832508
[1] "pi difference"
[1] 0.004801012
[1] "negative loglikelihood"
[1] 1547826
[1] "iteration"
[1] 39
[1] "phi difference"
[1] 0.002628865
[1] "pi difference"
[1] 0.004421177
[1] "negative loglikelihood"
[1] 1547814
[1] "iteration"
[1] 40
[1] "phi difference"
[1] 0.002435371
[1] "pi difference"
[1] 0.004077915
[1] "negative loglikelihood"
[1] 1547804
[1] "iteration"
[1] 41
[1] "phi difference"
[1] 0.002313386
[1] "pi difference"
[1] 0.003779616
[1] "negative loglikelihood"
[1] 1547795
[1] "iteration"
[1] 42
[1] "phi difference"
[1] 0.002123023
[1] "pi difference"
[1] 0.003526026
[1] "negative loglikelihood"
[1] 1547788
[1] "iteration"
[1] 43
[1] "phi difference"
[1] 0.001916216
[1] "pi difference"
[1] 0.003308955
[1] "negative loglikelihood"
[1] 1547781
[1] "iteration"
[1] 44
[1] "phi difference"
[1] 0.0017656
[1] "pi difference"
[1] 0.003110528
[1] "negative loglikelihood"
[1] 1547775
[1] "iteration"
[1] 45
[1] "phi difference"
[1] 0.001684359
[1] "pi difference"
[1] 0.002933182
[1] "negative loglikelihood"
[1] 1547770
[1] "iteration"
[1] 46
[1] "phi difference"
[1] 0.001585574
[1] "pi difference"
[1] 0.002770518
[1] "negative loglikelihood"
[1] 1547765
[1] "iteration"
[1] 47
[1] "phi difference"
[1] 0.0014518
[1] "pi difference"
[1] 0.002626192
[1] "negative loglikelihood"
[1] 1547760
[1] "iteration"
[1] 48
[1] "phi difference"
[1] 0.001385454
[1] "pi difference"
[1] 0.002498727
[1] "negative loglikelihood"
[1] 1547756
[1] "iteration"
[1] 49
[1] "phi difference"
[1] 0.001276966
[1] "pi difference"
[1] 0.002382345
[1] "negative loglikelihood"
[1] 1547752
[1] "iteration"
[1] 50
[1] "phi difference"
[1] 0.001177705
[1] "pi difference"
[1] 0.002276098
[1] "negative loglikelihood"
[1] 1547749
[1] "iteration"
[1] 51
[1] "phi difference"
[1] 0.001132947
[1] "pi difference"
[1] 0.002181821
[1] "negative loglikelihood"
[1] 1547745
[1] "iteration"
[1] 52
[1] "phi difference"
[1] 0.001090066
[1] "pi difference"
[1] 0.002095521
[1] "negative loglikelihood"
[1] 1547742
[1] "iteration"
[1] 53
[1] "phi difference"
[1] 0.001043696
[1] "pi difference"
[1] 0.002016015
[1] "negative loglikelihood"
[1] 1547739
[1] "iteration"
[1] 54
[1] "phi difference"
[1] 0.0009827324
[1] "pi difference"
[1] 0.001944414
[1] "negative loglikelihood"
[1] 1547736
[1] "iteration"
[1] 55
[1] "phi difference"
[1] 0.0009289521
[1] "pi difference"
[1] 0.001877975
[1] "negative loglikelihood"
[1] 1547734
[1] "iteration"
[1] 56
[1] "phi difference"
[1] 0.000876512
[1] "pi difference"
[1] 0.001816076
[1] "negative loglikelihood"
[1] 1547731
[1] "iteration"
[1] 57
[1] "phi difference"
[1] 0.0008307285
[1] "pi difference"
[1] 0.001759041
[1] "negative loglikelihood"
[1] 1547729
[1] "iteration"
[1] 58
[1] "phi difference"
[1] 0.0008034163
[1] "pi difference"
[1] 0.001704776
[1] "negative loglikelihood"
[1] 1547727
[1] "iteration"
[1] 59
[1] "phi difference"
[1] 0.0007853062
[1] "pi difference"
[1] 0.001653211
[1] "negative loglikelihood"
[1] 1547724
[1] "iteration"
[1] 60
[1] "phi difference"
[1] 0.0007481631
[1] "pi difference"
[1] 0.001605318
[1] "negative loglikelihood"
[1] 1547722
[1] "iteration"
[1] 61
[1] "phi difference"
[1] 0.0007088679
[1] "pi difference"
[1] 0.001560169
[1] "negative loglikelihood"
[1] 1547720
[1] "iteration"
[1] 62
[1] "phi difference"
[1] 0.0006779852
[1] "pi difference"
[1] 0.001518061
[1] "negative loglikelihood"
[1] 1547718
[1] "iteration"
[1] 63
[1] "phi difference"
[1] 0.0006566976
[1] "pi difference"
[1] 0.001477979
[1] "negative loglikelihood"
[1] 1547717
[1] "iteration"
[1] 64
[1] "phi difference"
[1] 0.0006547238
[1] "pi difference"
[1] 0.00144133
[1] "negative loglikelihood"
[1] 1547715
[1] "iteration"
[1] 65
[1] "phi difference"
[1] 0.0006487581
[1] "pi difference"
[1] 0.001407952
[1] "negative loglikelihood"
[1] 1547713
[1] "iteration"
[1] 66
[1] "phi difference"
[1] 0.0006353632
[1] "pi difference"
[1] 0.001376833
[1] "negative loglikelihood"
[1] 1547711
[1] "iteration"
[1] 67
[1] "phi difference"
[1] 0.000622759
[1] "pi difference"
[1] 0.001347232
[1] "negative loglikelihood"
[1] 1547710
[1] "iteration"
[1] 68
[1] "phi difference"
[1] 0.0006067917
[1] "pi difference"
[1] 0.001318114
[1] "negative loglikelihood"
[1] 1547708
[1] "iteration"
[1] 69
[1] "phi difference"
[1] 0.0005888941
[1] "pi difference"
[1] 0.001289981
[1] "negative loglikelihood"
[1] 1547707
[1] "iteration"
[1] 70
[1] "phi difference"
[1] 0.0005713779
[1] "pi difference"
[1] 0.001263342
[1] "negative loglikelihood"
[1] 1547706
[1] "iteration"
[1] 71
[1] "phi difference"
[1] 0.0005535687
[1] "pi difference"
[1] 0.001238107
[1] "negative loglikelihood"
[1] 1547704
[1] "iteration"
[1] 72
[1] "phi difference"
[1] 0.000536831
[1] "pi difference"
[1] 0.001213726
[1] "negative loglikelihood"
[1] 1547703
[1] "iteration"
[1] 73
[1] "phi difference"
[1] 0.0005223291
[1] "pi difference"
[1] 0.001190546
[1] "negative loglikelihood"
[1] 1547702
[1] "iteration"
[1] 74
[1] "phi difference"
[1] 0.000519353
[1] "pi difference"
[1] 0.001167923
[1] "negative loglikelihood"
[1] 1547700
[1] "iteration"
[1] 75
[1] "phi difference"
[1] 0.0005168541
[1] "pi difference"
[1] 0.001146075
[1] "negative loglikelihood"
[1] 1547699
[1] "iteration"
[1] 76
[1] "phi difference"
[1] 0.0005095154
[1] "pi difference"
[1] 0.001124777
[1] "negative loglikelihood"
[1] 1547698
[1] "iteration"
[1] 77
[1] "phi difference"
[1] 0.0004964102
[1] "pi difference"
[1] 0.001103644
[1] "negative loglikelihood"
[1] 1547697
[1] "iteration"
[1] 78
[1] "phi difference"
[1] 0.000482352
[1] "pi difference"
[1] 0.001083192
[1] "negative loglikelihood"
[1] 1547696
[1] "iteration"
[1] 79
[1] "phi difference"
[1] 0.0004789292
[1] "pi difference"
[1] 0.001063269
[1] "negative loglikelihood"
[1] 1547695
[1] "iteration"
[1] 80
[1] "phi difference"
[1] 0.0004761465
[1] "pi difference"
[1] 0.001044251
[1] "negative loglikelihood"
[1] 1547694
[1] "iteration"
[1] 81
[1] "phi difference"
[1] 0.0004733357
[1] "pi difference"
[1] 0.00102601
[1] "negative loglikelihood"
[1] 1547693
[1] "iteration"
[1] 82
[1] "phi difference"
[1] 0.0004692198
[1] "pi difference"
[1] 0.001008253
[1] "negative loglikelihood"
[1] 1547692
[1] "iteration"
[1] 83
[1] "phi difference"
[1] 0.000462306
[1] "pi difference"
[1] 0.000991118
[1] "negative loglikelihood"
[1] 1547691ploter(t(fit.gom$phi),main='gom')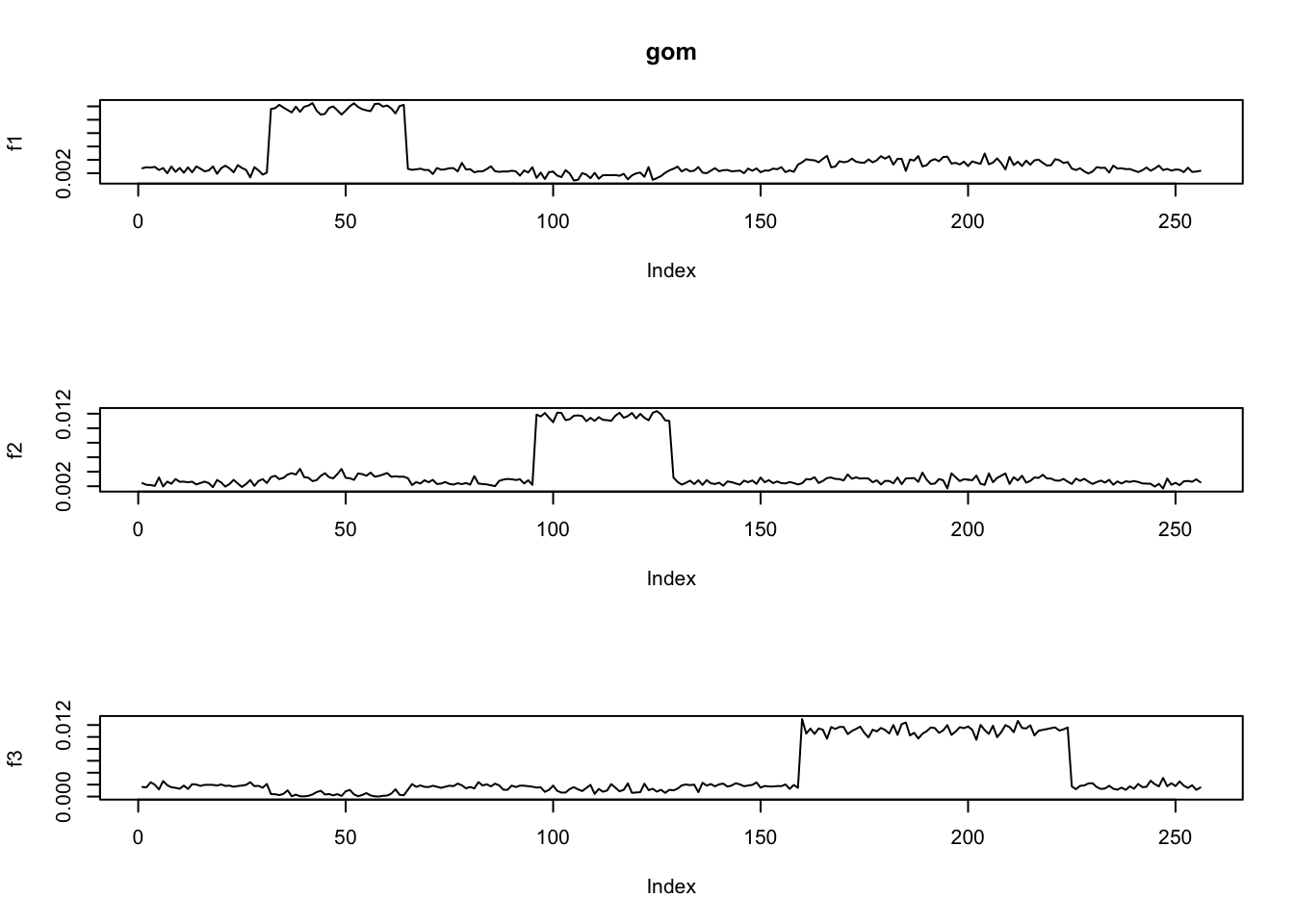
fit.stm = stm(y,K=3,nugget = TRUE,tol=1e-4)[1] "At iter 10, mean KL: 0.484295"ploter(fit.stm$EF,main='stm, scd-mkl')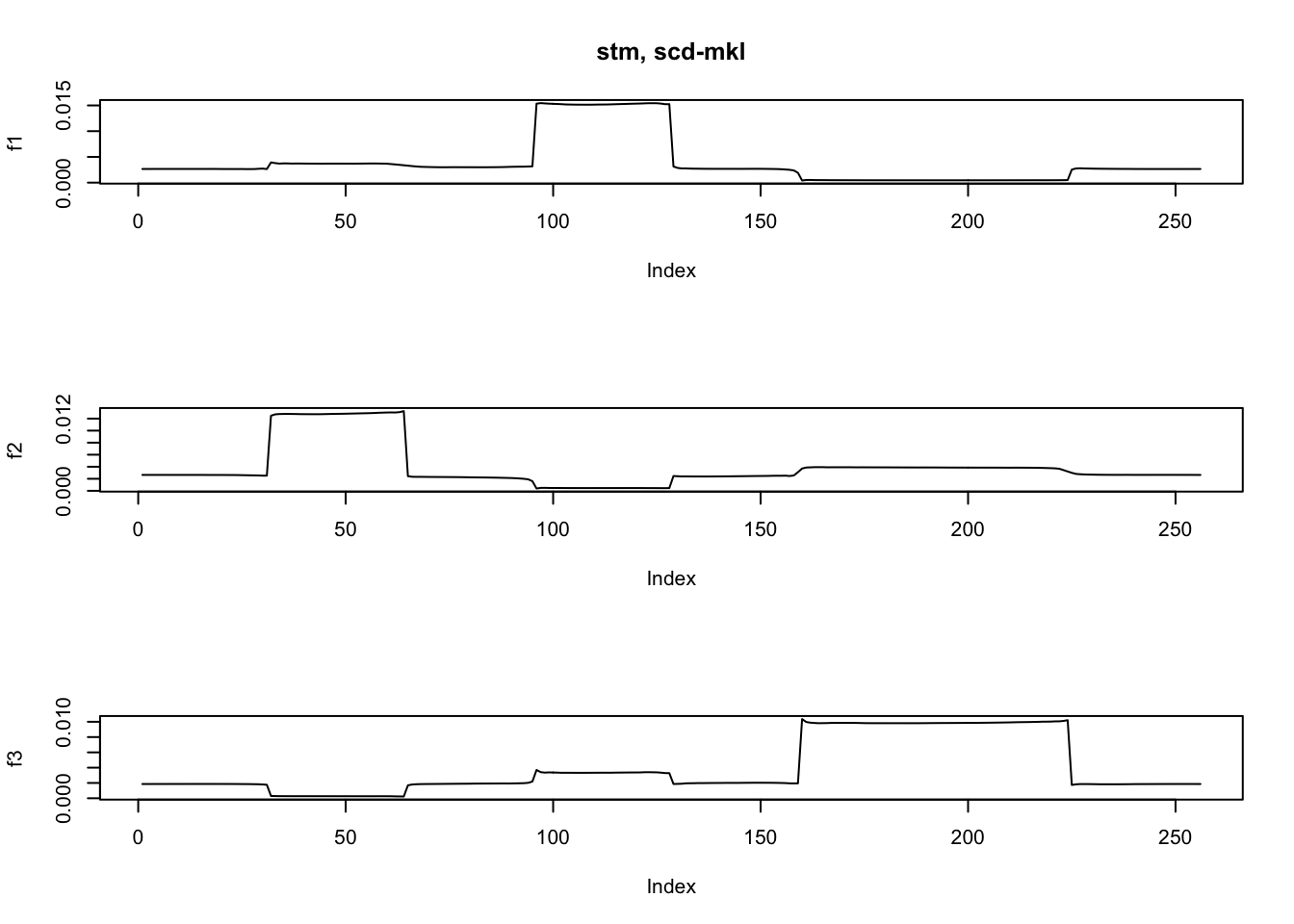
# change init
fit.stm2 = stm(y,K=3,nugget = TRUE,init='lee',tol=1e-4)
ploter(fit.stm2$EF,main='stm, lee-mkl')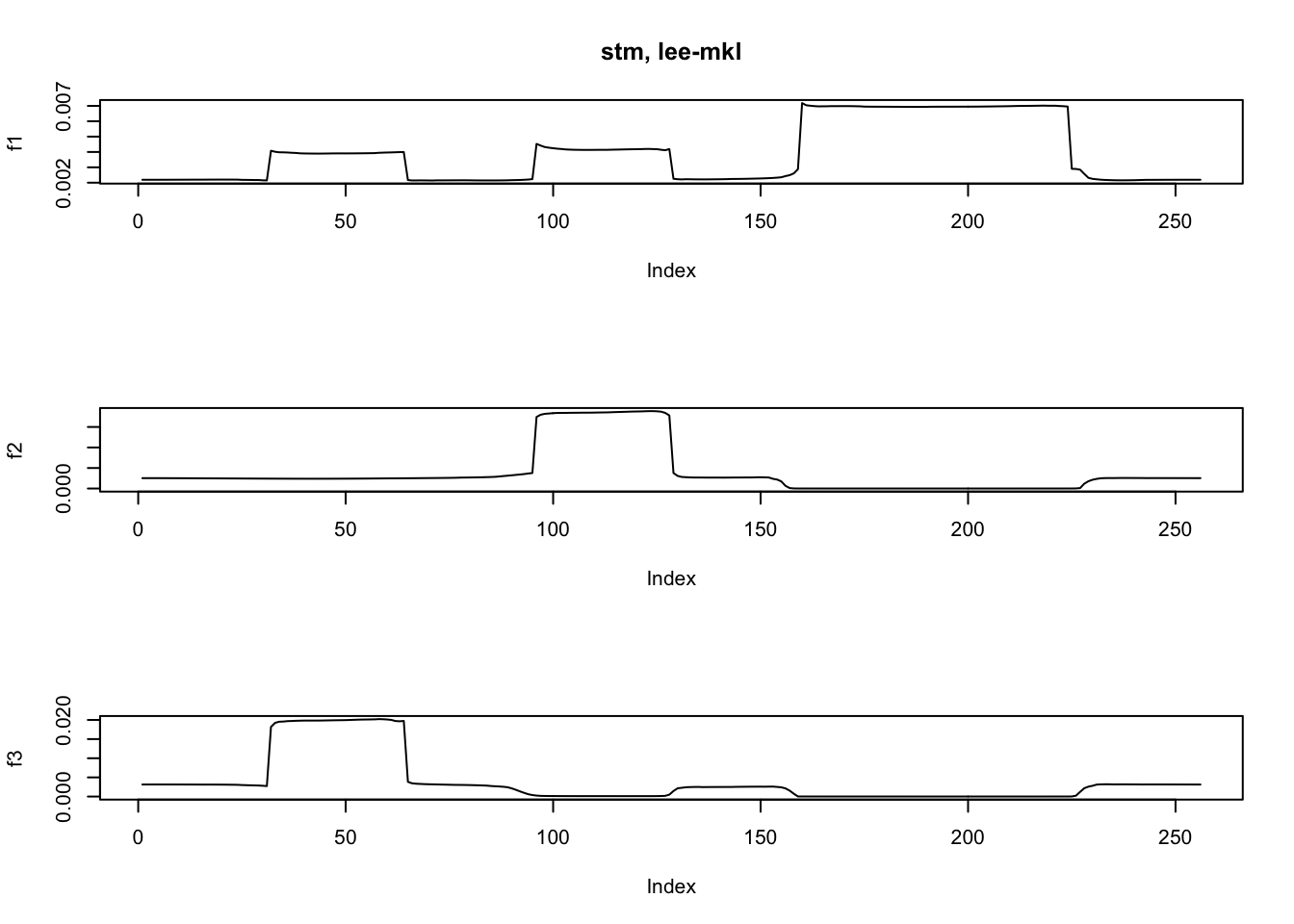
fit.stm3 = stm(y,K=3,nugget = TRUE,init='lee',init_loss = 'mse',tol=1e-4)[1] "At iter 10, mean KL: 0.492514"
[1] "At iter 20, mean KL: 0.490361"ploter(fit.stm3$EF,main='stm, lee-mse')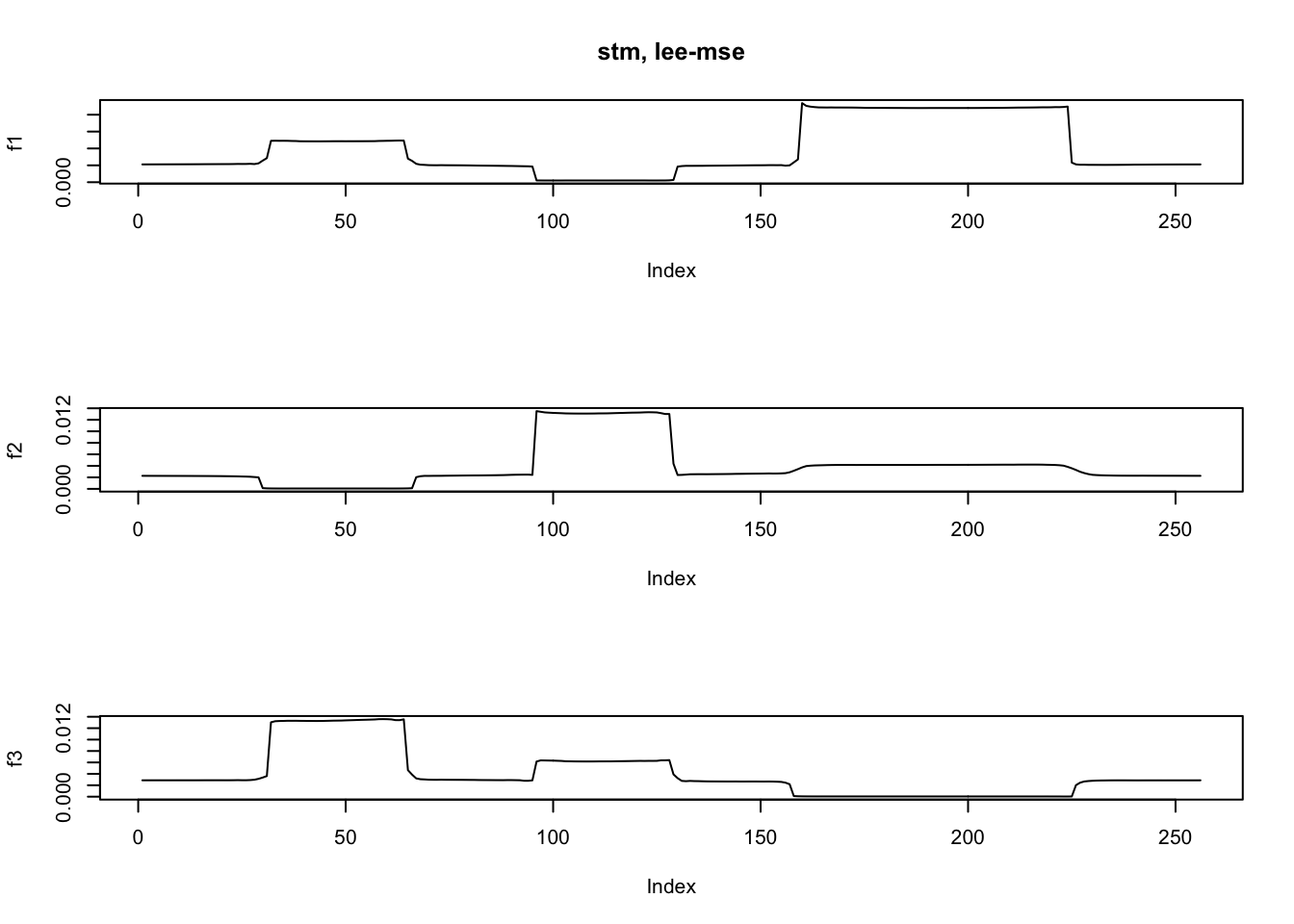
fit.stm4 = stm(y,K=3,nugget = TRUE,init='scd',init_loss = 'mse',tol=1e-4)[1] "At iter 10, mean KL: 0.484725"ploter(fit.stm4$EF,main='stm, scd-mse')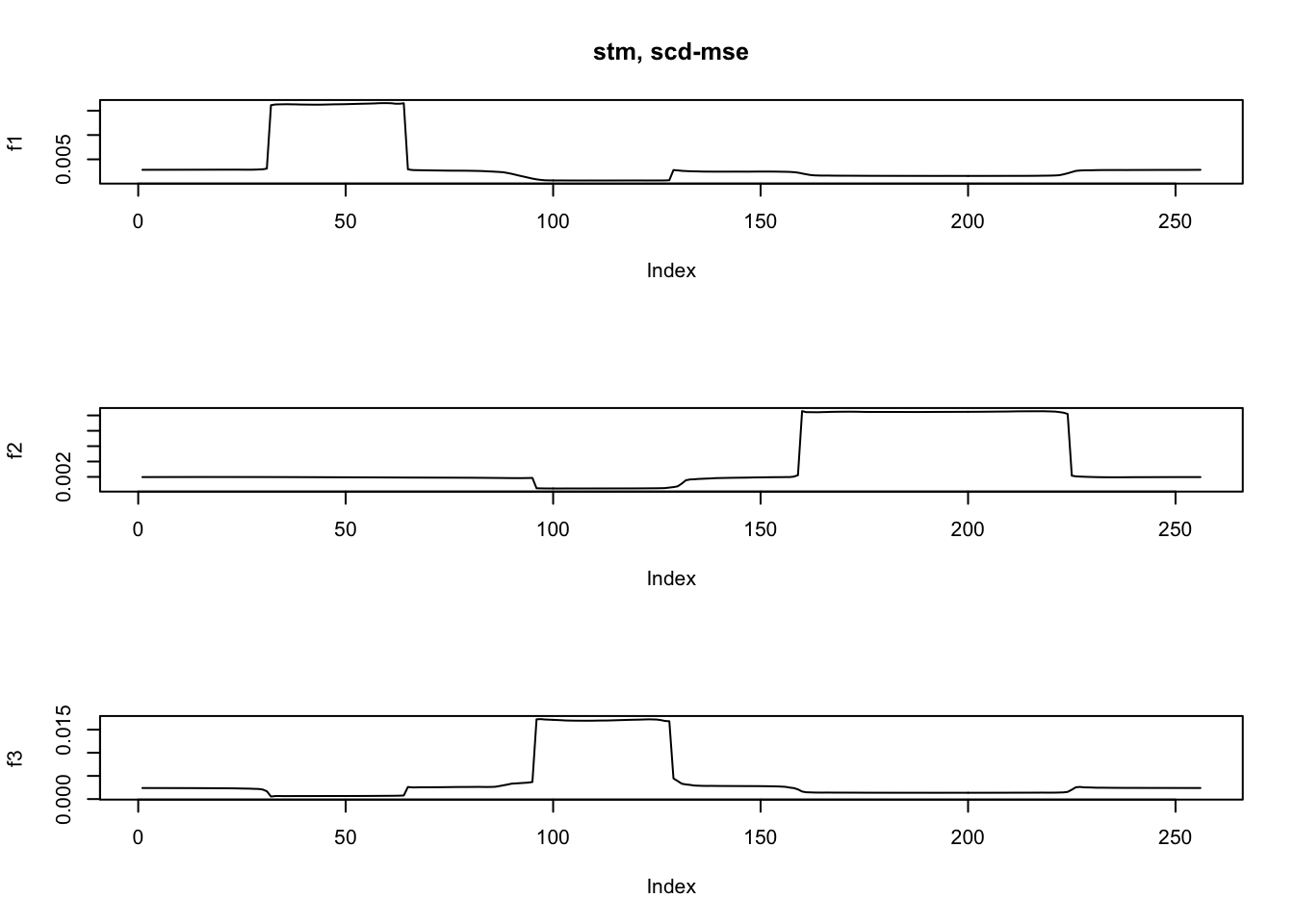
kmeans.init = kmeans(y, K, nstart = 5)
L0 = rep(1, n) %o% (as.vector(table(kmeans.init$cluster)))
F0 = t(kmeans.init$centers)
fit.stm5 = stm(y,K=3,nugget = TRUE,init = list(L_init=L0,F_init=F0),tol=1e-5)[1] "At iter 10, mean KL: 0.735056"
[1] "At iter 20, mean KL: 0.581710"
[1] "At iter 30, mean KL: 0.504752"
[1] "At iter 40, mean KL: 0.488120"
[1] "At iter 50, mean KL: 0.485984"
[1] "At iter 60, mean KL: 0.485408"ploter(fit.stm5$EF,main='stm, kmeans init')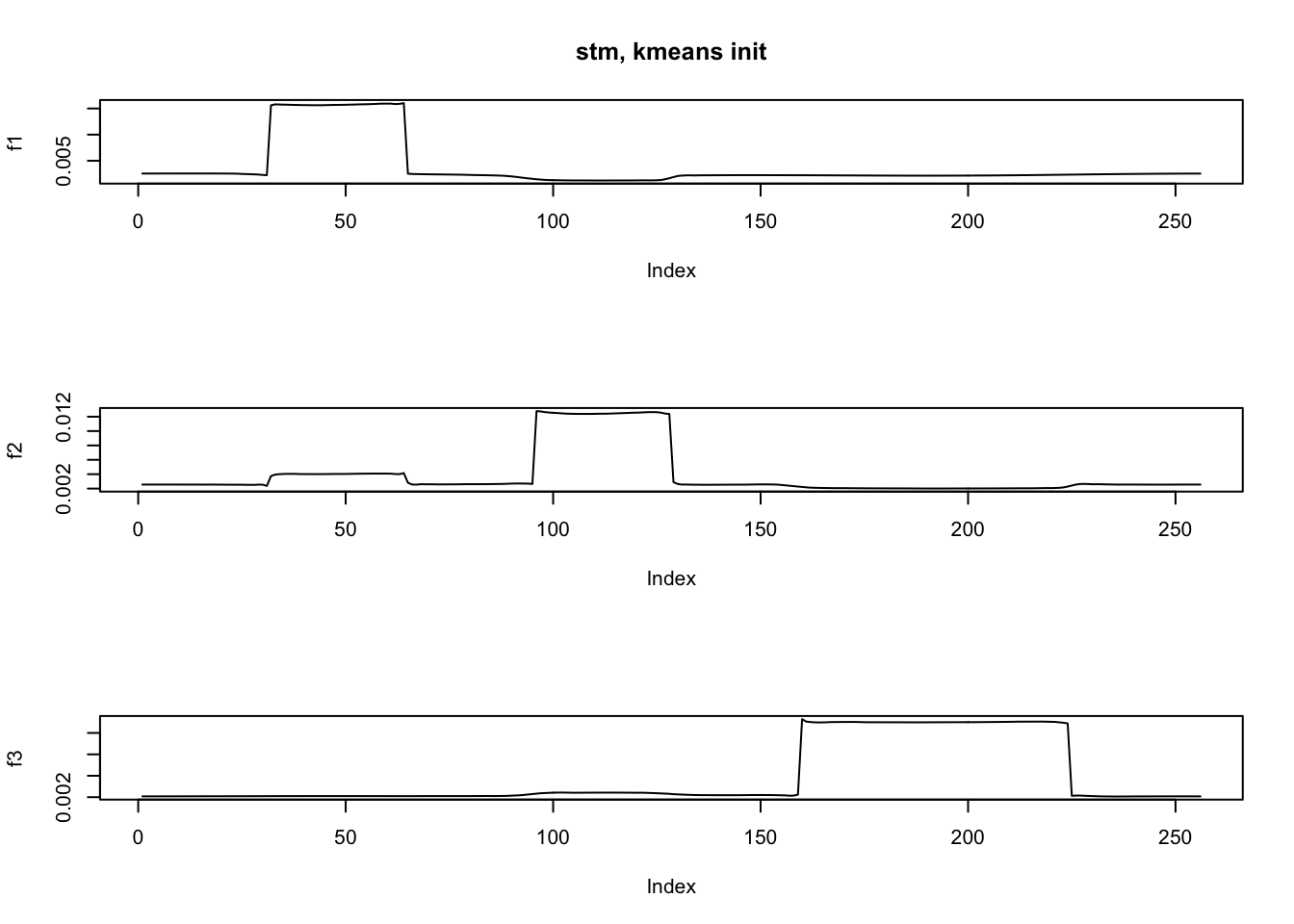
fit.sgom = cluster.mix(y,K=3,tol=1e-3,maxit = 100,nugget = T)[1] "iteration"
[1] 1
[1] "phi difference"
[1] 3988.373
[1] "pi difference"
[1] 0.2680048
[1] "negative loglikelihood"
[1] 1556268
[1] "iteration"
[1] 2
[1] "phi difference"
[1] 0.03018013
[1] "pi difference"
[1] 0.01787299
[1] "negative loglikelihood"
[1] 1556108
[1] "iteration"
[1] 3
[1] "phi difference"
[1] 0.03583746
[1] "pi difference"
[1] 0.01968614
[1] "negative loglikelihood"
[1] 1555875
[1] "iteration"
[1] 4
[1] "phi difference"
[1] 0.02971307
[1] "pi difference"
[1] 0.02180536
[1] "negative loglikelihood"
[1] 1555557
[1] "iteration"
[1] 5
[1] "phi difference"
[1] 0.03334056
[1] "pi difference"
[1] 0.02444069
[1] "negative loglikelihood"
[1] 1555135
[1] "iteration"
[1] 6
[1] "phi difference"
[1] 0.03854816
[1] "pi difference"
[1] 0.02713383
[1] "negative loglikelihood"
[1] 1554601
[1] "iteration"
[1] 7
[1] "phi difference"
[1] 0.04032402
[1] "pi difference"
[1] 0.02944567
[1] "negative loglikelihood"
[1] 1553963
[1] "iteration"
[1] 8
[1] "phi difference"
[1] 0.04240823
[1] "pi difference"
[1] 0.03053127
[1] "negative loglikelihood"
[1] 1553280
[1] "iteration"
[1] 9
[1] "phi difference"
[1] 0.04106111
[1] "pi difference"
[1] 0.03040469
[1] "negative loglikelihood"
[1] 1552617
[1] "iteration"
[1] 10
[1] "phi difference"
[1] 0.03786641
[1] "pi difference"
[1] 0.02946195
[1] "negative loglikelihood"
[1] 1552011
[1] "iteration"
[1] 11
[1] "phi difference"
[1] 0.03373034
[1] "pi difference"
[1] 0.027606
[1] "negative loglikelihood"
[1] 1551506
[1] "iteration"
[1] 12
[1] "phi difference"
[1] 0.02879371
[1] "pi difference"
[1] 0.02595568
[1] "negative loglikelihood"
[1] 1551079
[1] "iteration"
[1] 13
[1] "phi difference"
[1] 0.02232435
[1] "pi difference"
[1] 0.02443482
[1] "negative loglikelihood"
[1] 1550736
[1] "iteration"
[1] 14
[1] "phi difference"
[1] 0.01729528
[1] "pi difference"
[1] 0.02363252
[1] "negative loglikelihood"
[1] 1550436
[1] "iteration"
[1] 15
[1] "phi difference"
[1] 0.01573788
[1] "pi difference"
[1] 0.02302273
[1] "negative loglikelihood"
[1] 1550163
[1] "iteration"
[1] 16
[1] "phi difference"
[1] 0.01650664
[1] "pi difference"
[1] 0.02281812
[1] "negative loglikelihood"
[1] 1549905
[1] "iteration"
[1] 17
[1] "phi difference"
[1] 0.01569569
[1] "pi difference"
[1] 0.02260439
[1] "negative loglikelihood"
[1] 1549643
[1] "iteration"
[1] 18
[1] "phi difference"
[1] 0.01534902
[1] "pi difference"
[1] 0.02197915
[1] "negative loglikelihood"
[1] 1549392
[1] "iteration"
[1] 19
[1] "phi difference"
[1] 0.01487146
[1] "pi difference"
[1] 0.02118918
[1] "negative loglikelihood"
[1] 1549160
[1] "iteration"
[1] 20
[1] "phi difference"
[1] 0.01428396
[1] "pi difference"
[1] 0.0204687
[1] "negative loglikelihood"
[1] 1548948
[1] "iteration"
[1] 21
[1] "phi difference"
[1] 0.01085422
[1] "pi difference"
[1] 0.01886644
[1] "negative loglikelihood"
[1] 1548767
[1] "iteration"
[1] 22
[1] "phi difference"
[1] 0.009870626
[1] "pi difference"
[1] 0.01711367
[1] "negative loglikelihood"
[1] 1548623
[1] "iteration"
[1] 23
[1] "phi difference"
[1] 0.008548105
[1] "pi difference"
[1] 0.01540902
[1] "negative loglikelihood"
[1] 1548509
[1] "iteration"
[1] 24
[1] "phi difference"
[1] 0.008144208
[1] "pi difference"
[1] 0.01378699
[1] "negative loglikelihood"
[1] 1548420
[1] "iteration"
[1] 25
[1] "phi difference"
[1] 0.007262927
[1] "pi difference"
[1] 0.01223353
[1] "negative loglikelihood"
[1] 1548343
[1] "iteration"
[1] 26
[1] "phi difference"
[1] 0.006539517
[1] "pi difference"
[1] 0.01092857
[1] "negative loglikelihood"
[1] 1548288
[1] "iteration"
[1] 27
[1] "phi difference"
[1] 0.005962441
[1] "pi difference"
[1] 0.00977714
[1] "negative loglikelihood"
[1] 1548244
[1] "iteration"
[1] 28
[1] "phi difference"
[1] 0.00546834
[1] "pi difference"
[1] 0.008816407
[1] "negative loglikelihood"
[1] 1548209
[1] "iteration"
[1] 29
[1] "phi difference"
[1] 0.004964084
[1] "pi difference"
[1] 0.007863353
[1] "negative loglikelihood"
[1] 1548182
[1] "iteration"
[1] 30
[1] "phi difference"
[1] 0.004912835
[1] "pi difference"
[1] 0.007065226
[1] "negative loglikelihood"
[1] 1548160
[1] "iteration"
[1] 31
[1] "phi difference"
[1] 0.00475776
[1] "pi difference"
[1] 0.006406188
[1] "negative loglikelihood"
[1] 1548142
[1] "iteration"
[1] 32
[1] "phi difference"
[1] 0.004144307
[1] "pi difference"
[1] 0.005916537
[1] "negative loglikelihood"
[1] 1548120
[1] "iteration"
[1] 33
[1] "phi difference"
[1] 0.004228823
[1] "pi difference"
[1] 0.005429475
[1] "negative loglikelihood"
[1] 1548106
[1] "iteration"
[1] 34
[1] "phi difference"
[1] 0.004027642
[1] "pi difference"
[1] 0.005029188
[1] "negative loglikelihood"
[1] 1548094
[1] "iteration"
[1] 35
[1] "phi difference"
[1] 0.003329406
[1] "pi difference"
[1] 0.004679578
[1] "negative loglikelihood"
[1] 1548085
[1] "iteration"
[1] 36
[1] "phi difference"
[1] 0.002929253
[1] "pi difference"
[1] 0.004416778
[1] "negative loglikelihood"
[1] 1548076
[1] "iteration"
[1] 37
[1] "phi difference"
[1] 0.002634863
[1] "pi difference"
[1] 0.004199795
[1] "negative loglikelihood"
[1] 1548069
[1] "iteration"
[1] 38
[1] "phi difference"
[1] 0.002469349
[1] "pi difference"
[1] 0.0040106
[1] "negative loglikelihood"
[1] 1548062
[1] "iteration"
[1] 39
[1] "phi difference"
[1] 0.002484036
[1] "pi difference"
[1] 0.003840474
[1] "negative loglikelihood"
[1] 1548056
[1] "iteration"
[1] 40
[1] "phi difference"
[1] 0.002469018
[1] "pi difference"
[1] 0.003695681
[1] "negative loglikelihood"
[1] 1548050
[1] "iteration"
[1] 41
[1] "phi difference"
[1] 0.002469172
[1] "pi difference"
[1] 0.003566242
[1] "negative loglikelihood"
[1] 1548045
[1] "iteration"
[1] 42
[1] "phi difference"
[1] 0.002426261
[1] "pi difference"
[1] 0.003560945
[1] "negative loglikelihood"
[1] 1548034
[1] "iteration"
[1] 43
[1] "phi difference"
[1] 0.002401062
[1] "pi difference"
[1] 0.003394727
[1] "negative loglikelihood"
[1] 1548028
[1] "iteration"
[1] 44
[1] "phi difference"
[1] 0.002384302
[1] "pi difference"
[1] 0.003271703
[1] "negative loglikelihood"
[1] 1548024
[1] "iteration"
[1] 45
[1] "phi difference"
[1] 0.002353458
[1] "pi difference"
[1] 0.003167008
[1] "negative loglikelihood"
[1] 1548020
[1] "iteration"
[1] 46
[1] "phi difference"
[1] 0.002322013
[1] "pi difference"
[1] 0.003074777
[1] "negative loglikelihood"
[1] 1548016
[1] "iteration"
[1] 47
[1] "phi difference"
[1] 0.002284785
[1] "pi difference"
[1] 0.002990795
[1] "negative loglikelihood"
[1] 1548012
[1] "iteration"
[1] 48
[1] "phi difference"
[1] 0.002249176
[1] "pi difference"
[1] 0.002914901
[1] "negative loglikelihood"
[1] 1548008
[1] "iteration"
[1] 49
[1] "phi difference"
[1] 0.002215859
[1] "pi difference"
[1] 0.002850266
[1] "negative loglikelihood"
[1] 1548005
[1] "iteration"
[1] 50
[1] "phi difference"
[1] 0.00218779
[1] "pi difference"
[1] 0.002790675
[1] "negative loglikelihood"
[1] 1548002
[1] "iteration"
[1] 51
[1] "phi difference"
[1] 0.002158367
[1] "pi difference"
[1] 0.002736233
[1] "negative loglikelihood"
[1] 1547998
[1] "iteration"
[1] 52
[1] "phi difference"
[1] 0.002138825
[1] "pi difference"
[1] 0.002685156
[1] "negative loglikelihood"
[1] 1547995
[1] "iteration"
[1] 53
[1] "phi difference"
[1] 0.002110526
[1] "pi difference"
[1] 0.002638842
[1] "negative loglikelihood"
[1] 1547992
[1] "iteration"
[1] 54
[1] "phi difference"
[1] 0.002084028
[1] "pi difference"
[1] 0.002594762
[1] "negative loglikelihood"
[1] 1547989
[1] "iteration"
[1] 55
[1] "phi difference"
[1] 0.002059332
[1] "pi difference"
[1] 0.002552755
[1] "negative loglikelihood"
[1] 1547986
[1] "iteration"
[1] 56
[1] "phi difference"
[1] 0.002035167
[1] "pi difference"
[1] 0.002512751
[1] "negative loglikelihood"
[1] 1547984
[1] "iteration"
[1] 57
[1] "phi difference"
[1] 0.002012832
[1] "pi difference"
[1] 0.002476791
[1] "negative loglikelihood"
[1] 1547981
[1] "iteration"
[1] 58
[1] "phi difference"
[1] 0.001992535
[1] "pi difference"
[1] 0.002446409
[1] "negative loglikelihood"
[1] 1547978
[1] "iteration"
[1] 59
[1] "phi difference"
[1] 0.001974504
[1] "pi difference"
[1] 0.002419446
[1] "negative loglikelihood"
[1] 1547976
[1] "iteration"
[1] 60
[1] "phi difference"
[1] 0.001958425
[1] "pi difference"
[1] 0.002393076
[1] "negative loglikelihood"
[1] 1547973
[1] "iteration"
[1] 61
[1] "phi difference"
[1] 0.001989723
[1] "pi difference"
[1] 0.002276884
[1] "negative loglikelihood"
[1] 1547970
[1] "iteration"
[1] 62
[1] "phi difference"
[1] 0.001950623
[1] "pi difference"
[1] 0.002282698
[1] "negative loglikelihood"
[1] 1547968
[1] "iteration"
[1] 63
[1] "phi difference"
[1] 0.001923932
[1] "pi difference"
[1] 0.002268076
[1] "negative loglikelihood"
[1] 1547965
[1] "iteration"
[1] 64
[1] "phi difference"
[1] 0.001903519
[1] "pi difference"
[1] 0.002249296
[1] "negative loglikelihood"
[1] 1547963
[1] "iteration"
[1] 65
[1] "phi difference"
[1] 0.001904114
[1] "pi difference"
[1] 0.002228726
[1] "negative loglikelihood"
[1] 1547961
[1] "iteration"
[1] 66
[1] "phi difference"
[1] 0.001919569
[1] "pi difference"
[1] 0.002207453
[1] "negative loglikelihood"
[1] 1547959
[1] "iteration"
[1] 67
[1] "phi difference"
[1] 0.001924466
[1] "pi difference"
[1] 0.002185836
[1] "negative loglikelihood"
[1] 1547957
[1] "iteration"
[1] 68
[1] "phi difference"
[1] 0.001923349
[1] "pi difference"
[1] 0.002164205
[1] "negative loglikelihood"
[1] 1547955
[1] "iteration"
[1] 69
[1] "phi difference"
[1] 0.001917652
[1] "pi difference"
[1] 0.002142552
[1] "negative loglikelihood"
[1] 1547953
[1] "iteration"
[1] 70
[1] "phi difference"
[1] 0.00190977
[1] "pi difference"
[1] 0.002121029
[1] "negative loglikelihood"
[1] 1547951
[1] "iteration"
[1] 71
[1] "phi difference"
[1] 0.001896586
[1] "pi difference"
[1] 0.00209947
[1] "negative loglikelihood"
[1] 1547949
[1] "iteration"
[1] 72
[1] "phi difference"
[1] 0.00188439
[1] "pi difference"
[1] 0.00207807
[1] "negative loglikelihood"
[1] 1547947
[1] "iteration"
[1] 73
[1] "phi difference"
[1] 0.00186686
[1] "pi difference"
[1] 0.002057027
[1] "negative loglikelihood"
[1] 1547945
[1] "iteration"
[1] 74
[1] "phi difference"
[1] 0.001794007
[1] "pi difference"
[1] 0.001961822
[1] "negative loglikelihood"
[1] 1547943
[1] "iteration"
[1] 75
[1] "phi difference"
[1] 0.001738328
[1] "pi difference"
[1] 0.001960224
[1] "negative loglikelihood"
[1] 1547941
[1] "iteration"
[1] 76
[1] "phi difference"
[1] 0.00175927
[1] "pi difference"
[1] 0.001950683
[1] "negative loglikelihood"
[1] 1547940
[1] "iteration"
[1] 77
[1] "phi difference"
[1] 0.001760102
[1] "pi difference"
[1] 0.001935696
[1] "negative loglikelihood"
[1] 1547938
[1] "iteration"
[1] 78
[1] "phi difference"
[1] 0.001752297
[1] "pi difference"
[1] 0.00191842
[1] "negative loglikelihood"
[1] 1547936
[1] "iteration"
[1] 79
[1] "phi difference"
[1] 0.001739365
[1] "pi difference"
[1] 0.001900192
[1] "negative loglikelihood"
[1] 1547935
[1] "iteration"
[1] 80
[1] "phi difference"
[1] 0.001724546
[1] "pi difference"
[1] 0.001881809
[1] "negative loglikelihood"
[1] 1547933
[1] "iteration"
[1] 81
[1] "phi difference"
[1] 0.001735514
[1] "pi difference"
[1] 0.001863538
[1] "negative loglikelihood"
[1] 1547932
[1] "iteration"
[1] 82
[1] "phi difference"
[1] 0.001730098
[1] "pi difference"
[1] 0.001791939
[1] "negative loglikelihood"
[1] 1547929
[1] "iteration"
[1] 83
[1] "phi difference"
[1] 0.001727495
[1] "pi difference"
[1] 0.001770703
[1] "negative loglikelihood"
[1] 1547927
[1] "iteration"
[1] 84
[1] "phi difference"
[1] 0.001700501
[1] "pi difference"
[1] 0.001759386
[1] "negative loglikelihood"
[1] 1547926
[1] "iteration"
[1] 85
[1] "phi difference"
[1] 0.00167627
[1] "pi difference"
[1] 0.001749164
[1] "negative loglikelihood"
[1] 1547924
[1] "iteration"
[1] 86
[1] "phi difference"
[1] 0.001665829
[1] "pi difference"
[1] 0.001737654
[1] "negative loglikelihood"
[1] 1547923
[1] "iteration"
[1] 87
[1] "phi difference"
[1] 0.001672726
[1] "pi difference"
[1] 0.001688342
[1] "negative loglikelihood"
[1] 1547921
[1] "iteration"
[1] 88
[1] "phi difference"
[1] 0.001635966
[1] "pi difference"
[1] 0.001678322
[1] "negative loglikelihood"
[1] 1547919
[1] "iteration"
[1] 89
[1] "phi difference"
[1] 0.001498349
[1] "pi difference"
[1] 0.001596598
[1] "negative loglikelihood"
[1] 1547918
[1] "iteration"
[1] 90
[1] "phi difference"
[1] 0.001559974
[1] "pi difference"
[1] 0.001607123
[1] "negative loglikelihood"
[1] 1547917
[1] "iteration"
[1] 91
[1] "phi difference"
[1] 0.001558612
[1] "pi difference"
[1] 0.001608436
[1] "negative loglikelihood"
[1] 1547916
[1] "iteration"
[1] 92
[1] "phi difference"
[1] 0.001537687
[1] "pi difference"
[1] 0.001602466
[1] "negative loglikelihood"
[1] 1547914
[1] "iteration"
[1] 93
[1] "phi difference"
[1] 0.001515887
[1] "pi difference"
[1] 0.001592543
[1] "negative loglikelihood"
[1] 1547913
[1] "iteration"
[1] 94
[1] "phi difference"
[1] 0.001494541
[1] "pi difference"
[1] 0.001580507
[1] "negative loglikelihood"
[1] 1547912
[1] "iteration"
[1] 95
[1] "phi difference"
[1] 0.001473435
[1] "pi difference"
[1] 0.001567111
[1] "negative loglikelihood"
[1] 1547911
[1] "iteration"
[1] 96
[1] "phi difference"
[1] 0.001450557
[1] "pi difference"
[1] 0.001553231
[1] "negative loglikelihood"
[1] 1547910
[1] "iteration"
[1] 97
[1] "phi difference"
[1] 0.001431835
[1] "pi difference"
[1] 0.001539699
[1] "negative loglikelihood"
[1] 1547909
[1] "iteration"
[1] 98
[1] "phi difference"
[1] 0.001423584
[1] "pi difference"
[1] 0.001525928
[1] "negative loglikelihood"
[1] 1547908
[1] "iteration"
[1] 99
[1] "phi difference"
[1] 0.001398835
[1] "pi difference"
[1] 0.001492106
[1] "negative loglikelihood"
[1] 1547907
[1] "iteration"
[1] 100
[1] "phi difference"
[1] 0.001392031
[1] "pi difference"
[1] 0.001471048
[1] "negative loglikelihood"
[1] 1547906ploter(t(fit.sgom$phi),main='sgom, kmeans init')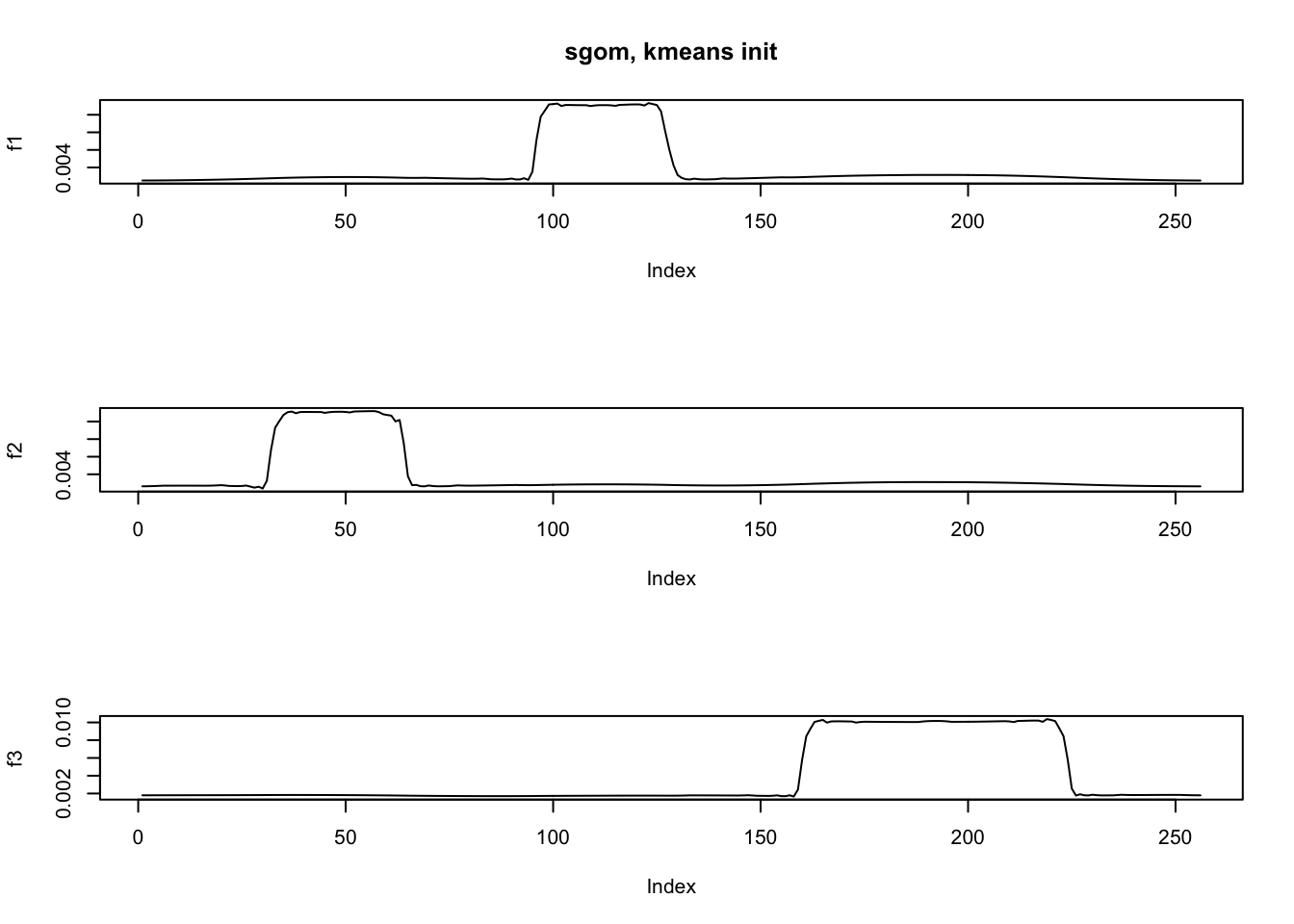
Now test two functions:
set.seed(123)
FFF = rbind(FF,FF)
y = matrix(rpois(n*p*2,tcrossprod(L,FFF)),nrow=n)
fit.stm = stm(y,K=3,nugget = TRUE,tol=1e-4,init='scd',init_loss = 'mkl')[1] "At iter 10, mean KL: 0.486996"
[1] "At iter 20, mean KL: 0.486484"
[1] "At iter 30, mean KL: 0.486346"
[1] "At iter 40, mean KL: 0.486644"
[1] "At iter 50, mean KL: 0.486525"
[1] "At iter 60, mean KL: 0.489061"ploter2(fit.stm$EF,main='stm, scd-mkl')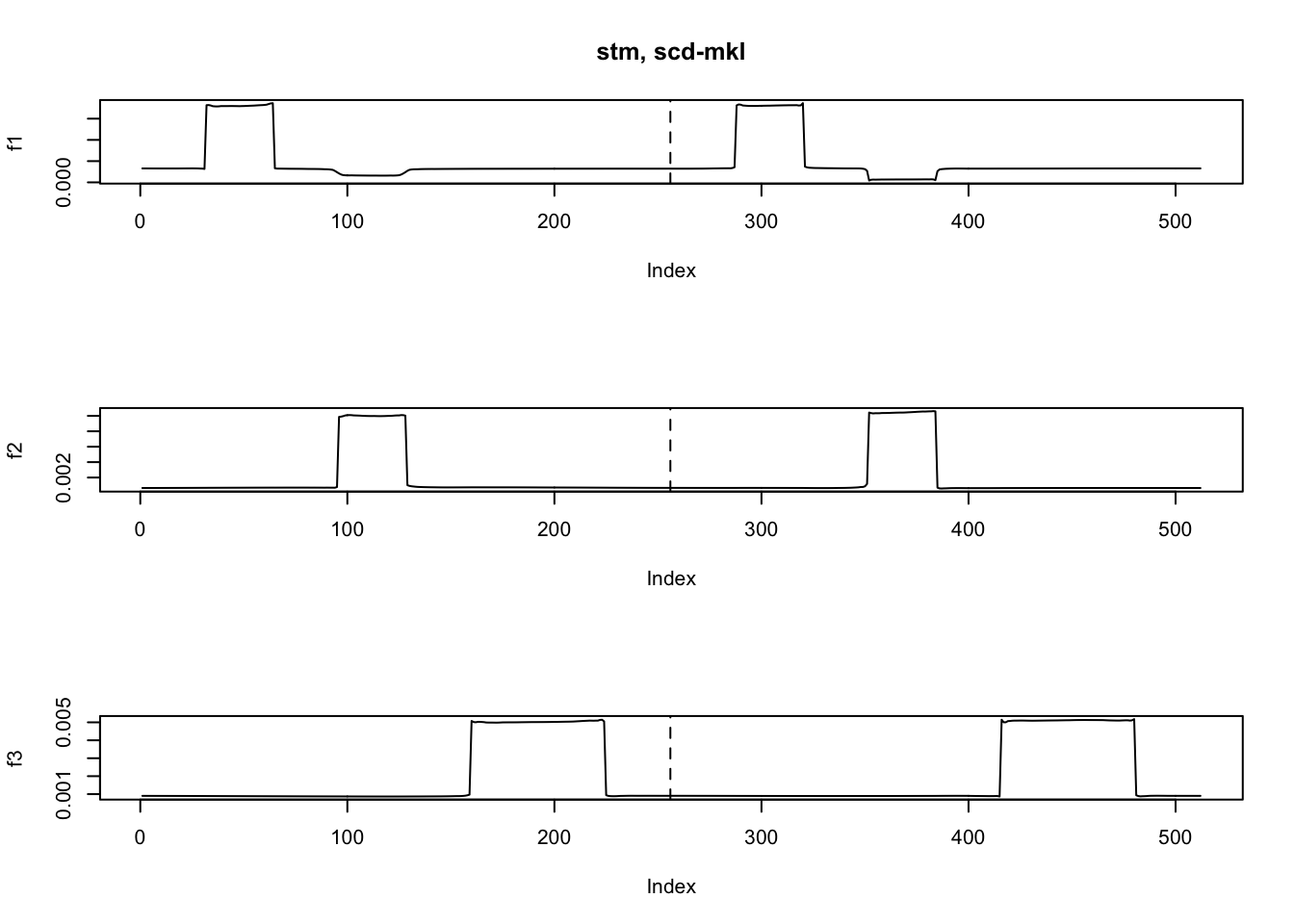
# change init
fit.stm2 = stm(y,K=3,nugget = TRUE,init='lee',init_loss = 'mkl',tol=1e-4)[1] "At iter 10, mean KL: 0.536938"ploter2(fit.stm2$EF,main='stm, lee-mkl')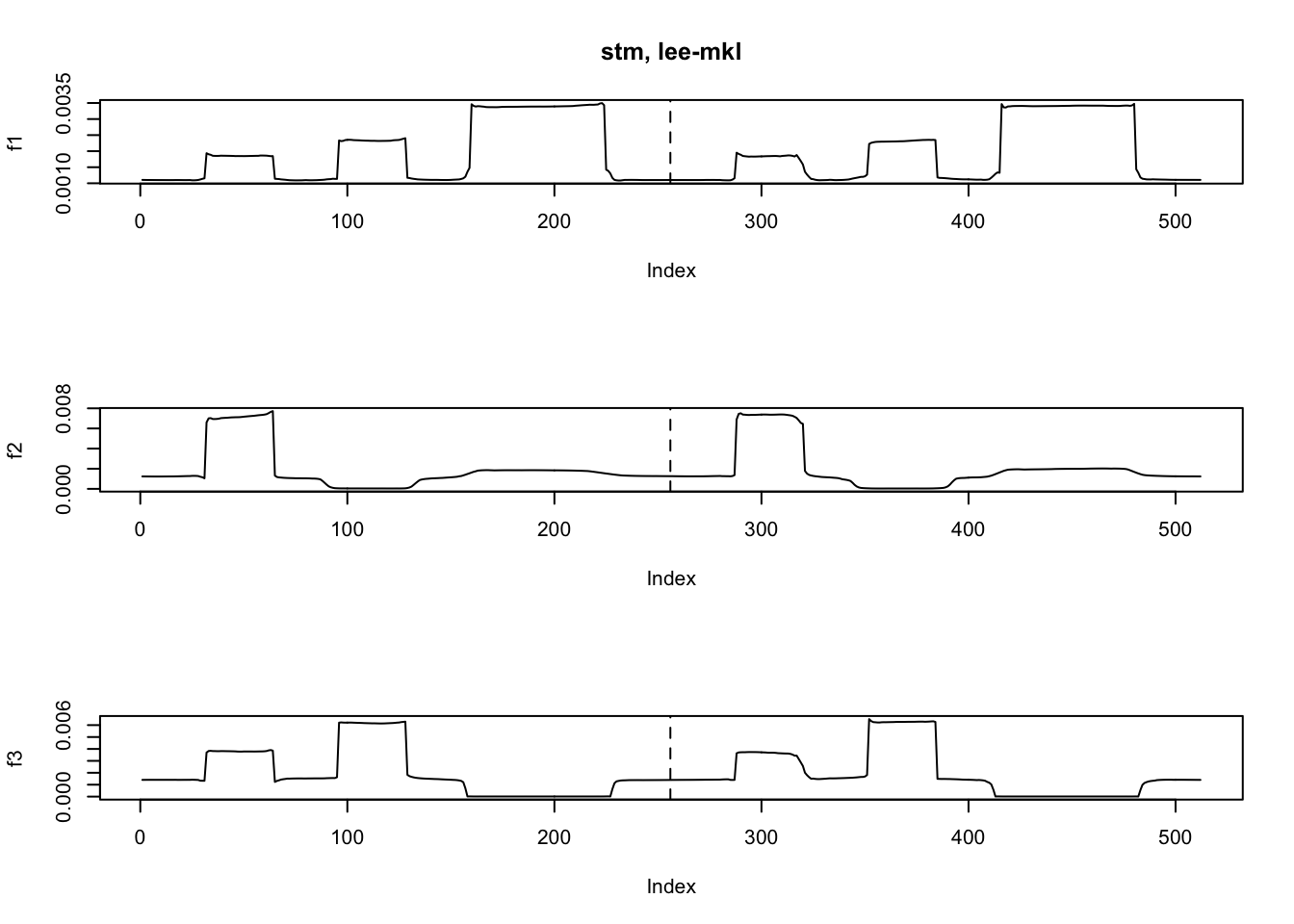
fit.stm3 = stm(y,K=3,nugget = TRUE,init='lee',init_loss = 'mse',tol=1e-4)
ploter2(fit.stm3$EF,main='stm, lee-mse')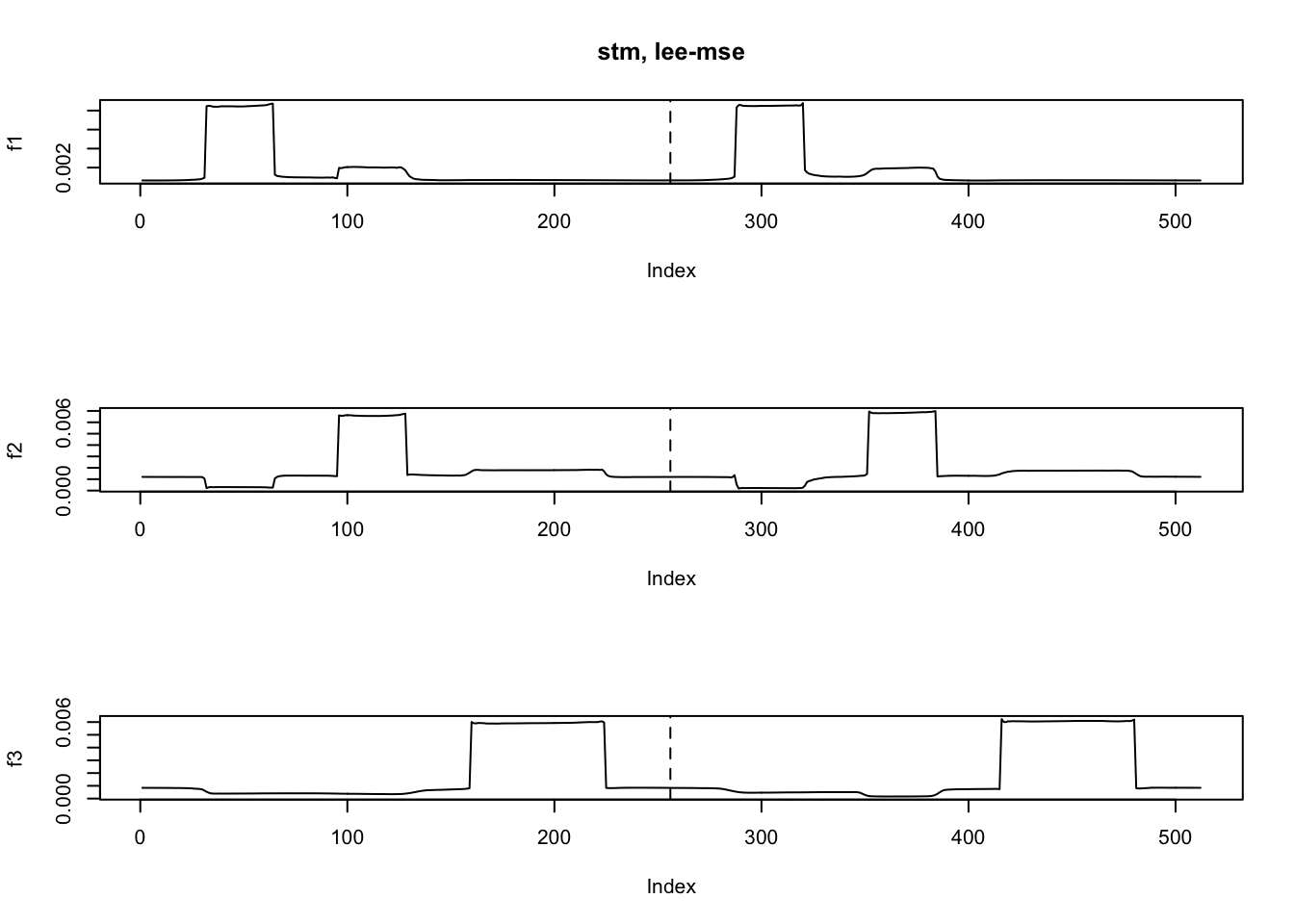
fit.stm4 = stm(y,K=3,nugget = TRUE,init='scd',init_loss = 'mse',tol=1e-4)[1] "At iter 10, mean KL: 0.488115"ploter2(fit.stm4$EF,main='stm, scd-mse')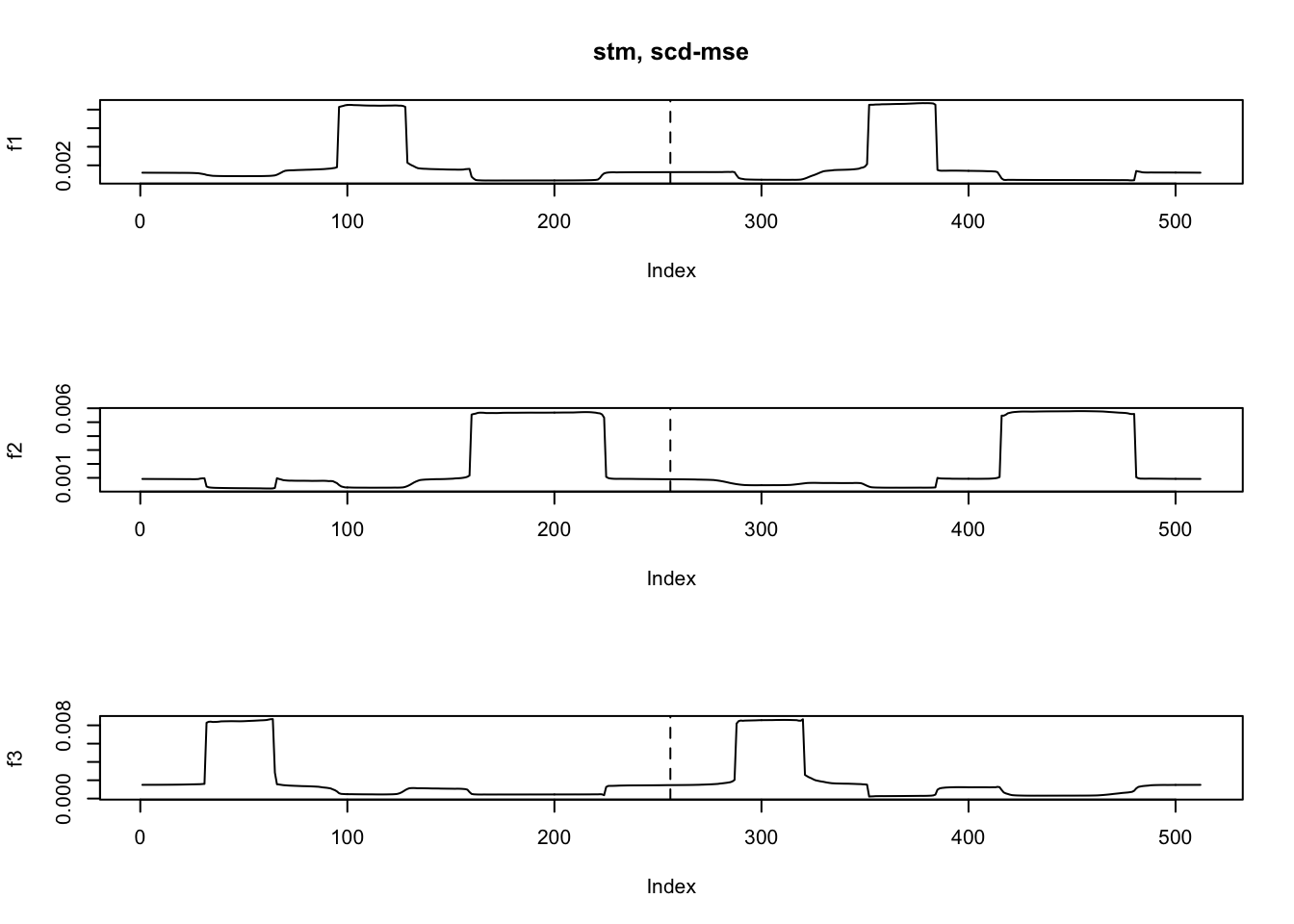
kmeans.init = kmeans(y, K, nstart = 20)
L0 = rep(1, n) %o% (as.vector(table(kmeans.init$cluster)))
F0 = t(kmeans.init$centers)
fit.stm5 = stm(y,K=3,nugget = TRUE,init = list(L_init=L0,F_init=F0),tol=1e-5)[1] "At iter 10, mean KL: 0.734644"
[1] "At iter 20, mean KL: 0.534781"
[1] "At iter 30, mean KL: 0.488247"
[1] "At iter 40, mean KL: 0.487026"
[1] "At iter 50, mean KL: 0.486390"
[1] "At iter 60, mean KL: 0.486425"
[1] "At iter 70, mean KL: 0.486102"ploter2(fit.stm5$EF,main='stm, kmeans init')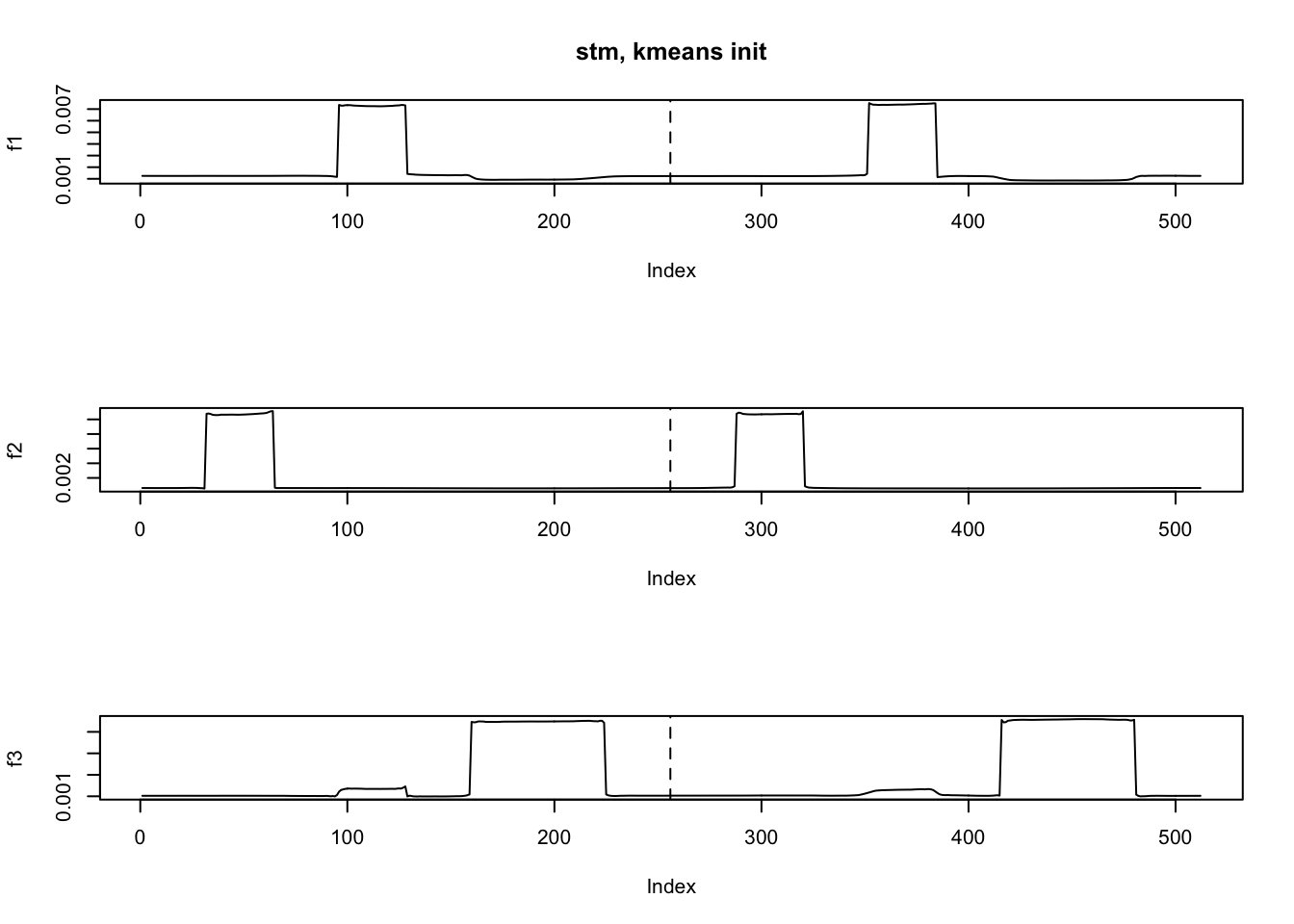
fit.sgom = cluster.mix(y,K=3,tol=1e-3,maxit = 100,nugget = T)[1] "iteration"
[1] 1
[1] "phi difference"
[1] 7892.405
[1] "pi difference"
[1] 0.2677622
[1] "negative loglikelihood"
[1] 3512295
[1] "iteration"
[1] 2
[1] "phi difference"
[1] 0.0379689
[1] "pi difference"
[1] 0.01846479
[1] "negative loglikelihood"
[1] 3511941
[1] "iteration"
[1] 3
[1] "phi difference"
[1] 0.0436682
[1] "pi difference"
[1] 0.02077947
[1] "negative loglikelihood"
[1] 3511407
[1] "iteration"
[1] 4
[1] "phi difference"
[1] 0.03650998
[1] "pi difference"
[1] 0.02381655
[1] "negative loglikelihood"
[1] 3510633
[1] "iteration"
[1] 5
[1] "phi difference"
[1] 0.03693277
[1] "pi difference"
[1] 0.02749967
[1] "negative loglikelihood"
[1] 3509585
[1] "iteration"
[1] 6
[1] "phi difference"
[1] 0.04406093
[1] "pi difference"
[1] 0.0311506
[1] "negative loglikelihood"
[1] 3508250
[1] "iteration"
[1] 7
[1] "phi difference"
[1] 0.04722812
[1] "pi difference"
[1] 0.03362491
[1] "negative loglikelihood"
[1] 3506706
[1] "iteration"
[1] 8
[1] "phi difference"
[1] 0.04678179
[1] "pi difference"
[1] 0.03461517
[1] "negative loglikelihood"
[1] 3505118
[1] "iteration"
[1] 9
[1] "phi difference"
[1] 0.0418353
[1] "pi difference"
[1] 0.03345156
[1] "negative loglikelihood"
[1] 3503694
[1] "iteration"
[1] 10
[1] "phi difference"
[1] 0.0348958
[1] "pi difference"
[1] 0.03177639
[1] "negative loglikelihood"
[1] 3502450
[1] "iteration"
[1] 11
[1] "phi difference"
[1] 0.0295633
[1] "pi difference"
[1] 0.0301965
[1] "negative loglikelihood"
[1] 3501407
[1] "iteration"
[1] 12
[1] "phi difference"
[1] 0.02444245
[1] "pi difference"
[1] 0.02907749
[1] "negative loglikelihood"
[1] 3500499
[1] "iteration"
[1] 13
[1] "phi difference"
[1] 0.02018698
[1] "pi difference"
[1] 0.0283852
[1] "negative loglikelihood"
[1] 3499704
[1] "iteration"
[1] 14
[1] "phi difference"
[1] 0.01704474
[1] "pi difference"
[1] 0.02711148
[1] "negative loglikelihood"
[1] 3499009
[1] "iteration"
[1] 15
[1] "phi difference"
[1] 0.01424221
[1] "pi difference"
[1] 0.02549777
[1] "negative loglikelihood"
[1] 3498402
[1] "iteration"
[1] 16
[1] "phi difference"
[1] 0.01838894
[1] "pi difference"
[1] 0.02367177
[1] "negative loglikelihood"
[1] 3497899
[1] "iteration"
[1] 17
[1] "phi difference"
[1] 0.02125098
[1] "pi difference"
[1] 0.02171565
[1] "negative loglikelihood"
[1] 3497491
[1] "iteration"
[1] 18
[1] "phi difference"
[1] 0.0219587
[1] "pi difference"
[1] 0.01983774
[1] "negative loglikelihood"
[1] 3497184
[1] "iteration"
[1] 19
[1] "phi difference"
[1] 0.01887537
[1] "pi difference"
[1] 0.01807375
[1] "negative loglikelihood"
[1] 3496939
[1] "iteration"
[1] 20
[1] "phi difference"
[1] 0.01265783
[1] "pi difference"
[1] 0.01620618
[1] "negative loglikelihood"
[1] 3496739
[1] "iteration"
[1] 21
[1] "phi difference"
[1] 0.01006968
[1] "pi difference"
[1] 0.01412676
[1] "negative loglikelihood"
[1] 3496593
[1] "iteration"
[1] 22
[1] "phi difference"
[1] 0.008018608
[1] "pi difference"
[1] 0.01257881
[1] "negative loglikelihood"
[1] 3496468
[1] "iteration"
[1] 23
[1] "phi difference"
[1] 0.006502438
[1] "pi difference"
[1] 0.01095633
[1] "negative loglikelihood"
[1] 3496377
[1] "iteration"
[1] 24
[1] "phi difference"
[1] 0.005221367
[1] "pi difference"
[1] 0.009596843
[1] "negative loglikelihood"
[1] 3496307
[1] "iteration"
[1] 25
[1] "phi difference"
[1] 0.004219676
[1] "pi difference"
[1] 0.008533203
[1] "negative loglikelihood"
[1] 3496249
[1] "iteration"
[1] 26
[1] "phi difference"
[1] 0.003955105
[1] "pi difference"
[1] 0.00755653
[1] "negative loglikelihood"
[1] 3496203
[1] "iteration"
[1] 27
[1] "phi difference"
[1] 0.002993657
[1] "pi difference"
[1] 0.0067356
[1] "negative loglikelihood"
[1] 3496165
[1] "iteration"
[1] 28
[1] "phi difference"
[1] 0.00267973
[1] "pi difference"
[1] 0.005984802
[1] "negative loglikelihood"
[1] 3496127
[1] "iteration"
[1] 29
[1] "phi difference"
[1] 0.00212502
[1] "pi difference"
[1] 0.005393021
[1] "negative loglikelihood"
[1] 3496097
[1] "iteration"
[1] 30
[1] "phi difference"
[1] 0.002279228
[1] "pi difference"
[1] 0.004940119
[1] "negative loglikelihood"
[1] 3496074
[1] "iteration"
[1] 31
[1] "phi difference"
[1] 0.002407007
[1] "pi difference"
[1] 0.004583082
[1] "negative loglikelihood"
[1] 3496055
[1] "iteration"
[1] 32
[1] "phi difference"
[1] 0.002479638
[1] "pi difference"
[1] 0.004311338
[1] "negative loglikelihood"
[1] 3496038
[1] "iteration"
[1] 33
[1] "phi difference"
[1] 0.002545767
[1] "pi difference"
[1] 0.004099626
[1] "negative loglikelihood"
[1] 3496023
[1] "iteration"
[1] 34
[1] "phi difference"
[1] 0.002551584
[1] "pi difference"
[1] 0.003904647
[1] "negative loglikelihood"
[1] 3496010
[1] "iteration"
[1] 35
[1] "phi difference"
[1] 0.002546811
[1] "pi difference"
[1] 0.003741738
[1] "negative loglikelihood"
[1] 3495997
[1] "iteration"
[1] 36
[1] "phi difference"
[1] 0.002536208
[1] "pi difference"
[1] 0.003587549
[1] "negative loglikelihood"
[1] 3495985
[1] "iteration"
[1] 37
[1] "phi difference"
[1] 0.002538028
[1] "pi difference"
[1] 0.003447868
[1] "negative loglikelihood"
[1] 3495975
[1] "iteration"
[1] 38
[1] "phi difference"
[1] 0.002511125
[1] "pi difference"
[1] 0.00332751
[1] "negative loglikelihood"
[1] 3495964
[1] "iteration"
[1] 39
[1] "phi difference"
[1] 0.002485373
[1] "pi difference"
[1] 0.003217536
[1] "negative loglikelihood"
[1] 3495955
[1] "iteration"
[1] 40
[1] "phi difference"
[1] 0.002447365
[1] "pi difference"
[1] 0.003120623
[1] "negative loglikelihood"
[1] 3495946
[1] "iteration"
[1] 41
[1] "phi difference"
[1] 0.002414424
[1] "pi difference"
[1] 0.003035548
[1] "negative loglikelihood"
[1] 3495937
[1] "iteration"
[1] 42
[1] "phi difference"
[1] 0.002390708
[1] "pi difference"
[1] 0.002961346
[1] "negative loglikelihood"
[1] 3495929
[1] "iteration"
[1] 43
[1] "phi difference"
[1] 0.002382012
[1] "pi difference"
[1] 0.002892438
[1] "negative loglikelihood"
[1] 3495921
[1] "iteration"
[1] 44
[1] "phi difference"
[1] 0.002331953
[1] "pi difference"
[1] 0.002837581
[1] "negative loglikelihood"
[1] 3495913
[1] "iteration"
[1] 45
[1] "phi difference"
[1] 0.002315162
[1] "pi difference"
[1] 0.002792455
[1] "negative loglikelihood"
[1] 3495905
[1] "iteration"
[1] 46
[1] "phi difference"
[1] 0.002298546
[1] "pi difference"
[1] 0.002754093
[1] "negative loglikelihood"
[1] 3495898
[1] "iteration"
[1] 47
[1] "phi difference"
[1] 0.002281809
[1] "pi difference"
[1] 0.002718074
[1] "negative loglikelihood"
[1] 3495891
[1] "iteration"
[1] 48
[1] "phi difference"
[1] 0.002249297
[1] "pi difference"
[1] 0.00268596
[1] "negative loglikelihood"
[1] 3495884
[1] "iteration"
[1] 49
[1] "phi difference"
[1] 0.002257303
[1] "pi difference"
[1] 0.002654853
[1] "negative loglikelihood"
[1] 3495877
[1] "iteration"
[1] 50
[1] "phi difference"
[1] 0.002254351
[1] "pi difference"
[1] 0.002629907
[1] "negative loglikelihood"
[1] 3495871
[1] "iteration"
[1] 51
[1] "phi difference"
[1] 0.002243879
[1] "pi difference"
[1] 0.002608092
[1] "negative loglikelihood"
[1] 3495865
[1] "iteration"
[1] 52
[1] "phi difference"
[1] 0.002215963
[1] "pi difference"
[1] 0.002541874
[1] "negative loglikelihood"
[1] 3495857
[1] "iteration"
[1] 53
[1] "phi difference"
[1] 0.002200637
[1] "pi difference"
[1] 0.002543268
[1] "negative loglikelihood"
[1] 3495851
[1] "iteration"
[1] 54
[1] "phi difference"
[1] 0.002187092
[1] "pi difference"
[1] 0.002538508
[1] "negative loglikelihood"
[1] 3495845
[1] "iteration"
[1] 55
[1] "phi difference"
[1] 0.002189963
[1] "pi difference"
[1] 0.002490186
[1] "negative loglikelihood"
[1] 3495839
[1] "iteration"
[1] 56
[1] "phi difference"
[1] 0.002156809
[1] "pi difference"
[1] 0.002473204
[1] "negative loglikelihood"
[1] 3495833
[1] "iteration"
[1] 57
[1] "phi difference"
[1] 0.002127963
[1] "pi difference"
[1] 0.002444326
[1] "negative loglikelihood"
[1] 3495828
[1] "iteration"
[1] 58
[1] "phi difference"
[1] 0.002095303
[1] "pi difference"
[1] 0.002405296
[1] "negative loglikelihood"
[1] 3495822
[1] "iteration"
[1] 59
[1] "phi difference"
[1] 0.00209071
[1] "pi difference"
[1] 0.002397739
[1] "negative loglikelihood"
[1] 3495816
[1] "iteration"
[1] 60
[1] "phi difference"
[1] 0.002062004
[1] "pi difference"
[1] 0.002384365
[1] "negative loglikelihood"
[1] 3495811
[1] "iteration"
[1] 61
[1] "phi difference"
[1] 0.002071835
[1] "pi difference"
[1] 0.002363512
[1] "negative loglikelihood"
[1] 3495806
[1] "iteration"
[1] 62
[1] "phi difference"
[1] 0.002041922
[1] "pi difference"
[1] 0.002328577
[1] "negative loglikelihood"
[1] 3495802
[1] "iteration"
[1] 63
[1] "phi difference"
[1] 0.002021581
[1] "pi difference"
[1] 0.002317958
[1] "negative loglikelihood"
[1] 3495797
[1] "iteration"
[1] 64
[1] "phi difference"
[1] 0.00196265
[1] "pi difference"
[1] 0.002295939
[1] "negative loglikelihood"
[1] 3495793
[1] "iteration"
[1] 65
[1] "phi difference"
[1] 0.001984323
[1] "pi difference"
[1] 0.002280442
[1] "negative loglikelihood"
[1] 3495788
[1] "iteration"
[1] 66
[1] "phi difference"
[1] 0.001930945
[1] "pi difference"
[1] 0.002236811
[1] "negative loglikelihood"
[1] 3495782
[1] "iteration"
[1] 67
[1] "phi difference"
[1] 0.001934175
[1] "pi difference"
[1] 0.002222583
[1] "negative loglikelihood"
[1] 3495778
[1] "iteration"
[1] 68
[1] "phi difference"
[1] 0.001921063
[1] "pi difference"
[1] 0.002208974
[1] "negative loglikelihood"
[1] 3495773
[1] "iteration"
[1] 69
[1] "phi difference"
[1] 0.001925458
[1] "pi difference"
[1] 0.002192477
[1] "negative loglikelihood"
[1] 3495769
[1] "iteration"
[1] 70
[1] "phi difference"
[1] 0.001945061
[1] "pi difference"
[1] 0.00213395
[1] "negative loglikelihood"
[1] 3495765
[1] "iteration"
[1] 71
[1] "phi difference"
[1] 0.00186265
[1] "pi difference"
[1] 0.002064106
[1] "negative loglikelihood"
[1] 3495761
[1] "iteration"
[1] 72
[1] "phi difference"
[1] 0.001815166
[1] "pi difference"
[1] 0.002081738
[1] "negative loglikelihood"
[1] 3495757
[1] "iteration"
[1] 73
[1] "phi difference"
[1] 0.00181396
[1] "pi difference"
[1] 0.002074656
[1] "negative loglikelihood"
[1] 3495753
[1] "iteration"
[1] 74
[1] "phi difference"
[1] 0.001813777
[1] "pi difference"
[1] 0.002060524
[1] "negative loglikelihood"
[1] 3495749
[1] "iteration"
[1] 75
[1] "phi difference"
[1] 0.001880053
[1] "pi difference"
[1] 0.00195965
[1] "negative loglikelihood"
[1] 3495747
[1] "iteration"
[1] 76
[1] "phi difference"
[1] 0.001822667
[1] "pi difference"
[1] 0.001979323
[1] "negative loglikelihood"
[1] 3495744
[1] "iteration"
[1] 77
[1] "phi difference"
[1] 0.001727907
[1] "pi difference"
[1] 0.001942758
[1] "negative loglikelihood"
[1] 3495740
[1] "iteration"
[1] 78
[1] "phi difference"
[1] 0.001689524
[1] "pi difference"
[1] 0.001931267
[1] "negative loglikelihood"
[1] 3495736
[1] "iteration"
[1] 79
[1] "phi difference"
[1] 0.001689444
[1] "pi difference"
[1] 0.001927212
[1] "negative loglikelihood"
[1] 3495732
[1] "iteration"
[1] 80
[1] "phi difference"
[1] 0.001679536
[1] "pi difference"
[1] 0.001717146
[1] "negative loglikelihood"
[1] 3495722
[1] "iteration"
[1] 81
[1] "phi difference"
[1] 0.001661715
[1] "pi difference"
[1] 0.001826611
[1] "negative loglikelihood"
[1] 3495718
[1] "iteration"
[1] 82
[1] "phi difference"
[1] 0.00168135
[1] "pi difference"
[1] 0.001817015
[1] "negative loglikelihood"
[1] 3495715
[1] "iteration"
[1] 83
[1] "phi difference"
[1] 0.001658501
[1] "pi difference"
[1] 0.001814753
[1] "negative loglikelihood"
[1] 3495712
[1] "iteration"
[1] 84
[1] "phi difference"
[1] 0.001633717
[1] "pi difference"
[1] 0.00179768
[1] "negative loglikelihood"
[1] 3495709
[1] "iteration"
[1] 85
[1] "phi difference"
[1] 0.001574049
[1] "pi difference"
[1] 0.001626841
[1] "negative loglikelihood"
[1] 3495699
[1] "iteration"
[1] 86
[1] "phi difference"
[1] 0.001610495
[1] "pi difference"
[1] 0.001707527
[1] "negative loglikelihood"
[1] 3495696
[1] "iteration"
[1] 87
[1] "phi difference"
[1] 0.001547156
[1] "pi difference"
[1] 0.001686927
[1] "negative loglikelihood"
[1] 3495693
[1] "iteration"
[1] 88
[1] "phi difference"
[1] 0.001537362
[1] "pi difference"
[1] 0.001700788
[1] "negative loglikelihood"
[1] 3495690
[1] "iteration"
[1] 89
[1] "phi difference"
[1] 0.001507697
[1] "pi difference"
[1] 0.001698673
[1] "negative loglikelihood"
[1] 3495687
[1] "iteration"
[1] 90
[1] "phi difference"
[1] 0.001480216
[1] "pi difference"
[1] 0.001689763
[1] "negative loglikelihood"
[1] 3495685
[1] "iteration"
[1] 91
[1] "phi difference"
[1] 0.001453214
[1] "pi difference"
[1] 0.001678377
[1] "negative loglikelihood"
[1] 3495682
[1] "iteration"
[1] 92
[1] "phi difference"
[1] 0.001412847
[1] "pi difference"
[1] 0.001665663
[1] "negative loglikelihood"
[1] 3495680
[1] "iteration"
[1] 93
[1] "phi difference"
[1] 0.001410081
[1] "pi difference"
[1] 0.001647452
[1] "negative loglikelihood"
[1] 3495678
[1] "iteration"
[1] 94
[1] "phi difference"
[1] 0.001427167
[1] "pi difference"
[1] 0.001612153
[1] "negative loglikelihood"
[1] 3495674
[1] "iteration"
[1] 95
[1] "phi difference"
[1] 0.001433414
[1] "pi difference"
[1] 0.001581008
[1] "negative loglikelihood"
[1] 3495672
[1] "iteration"
[1] 96
[1] "phi difference"
[1] 0.001406101
[1] "pi difference"
[1] 0.001578095
[1] "negative loglikelihood"
[1] 3495670
[1] "iteration"
[1] 97
[1] "phi difference"
[1] 0.00143738
[1] "pi difference"
[1] 0.001524344
[1] "negative loglikelihood"
[1] 3495668
[1] "iteration"
[1] 98
[1] "phi difference"
[1] 0.001391724
[1] "pi difference"
[1] 0.001534715
[1] "negative loglikelihood"
[1] 3495666
[1] "iteration"
[1] 99
[1] "phi difference"
[1] 0.001370973
[1] "pi difference"
[1] 0.001530443
[1] "negative loglikelihood"
[1] 3495664
[1] "iteration"
[1] 100
[1] "phi difference"
[1] 0.001375036
[1] "pi difference"
[1] 0.001477857
[1] "negative loglikelihood"
[1] 3495662ploter2(t(fit.sgom$phi),main='sgom, kmeans init')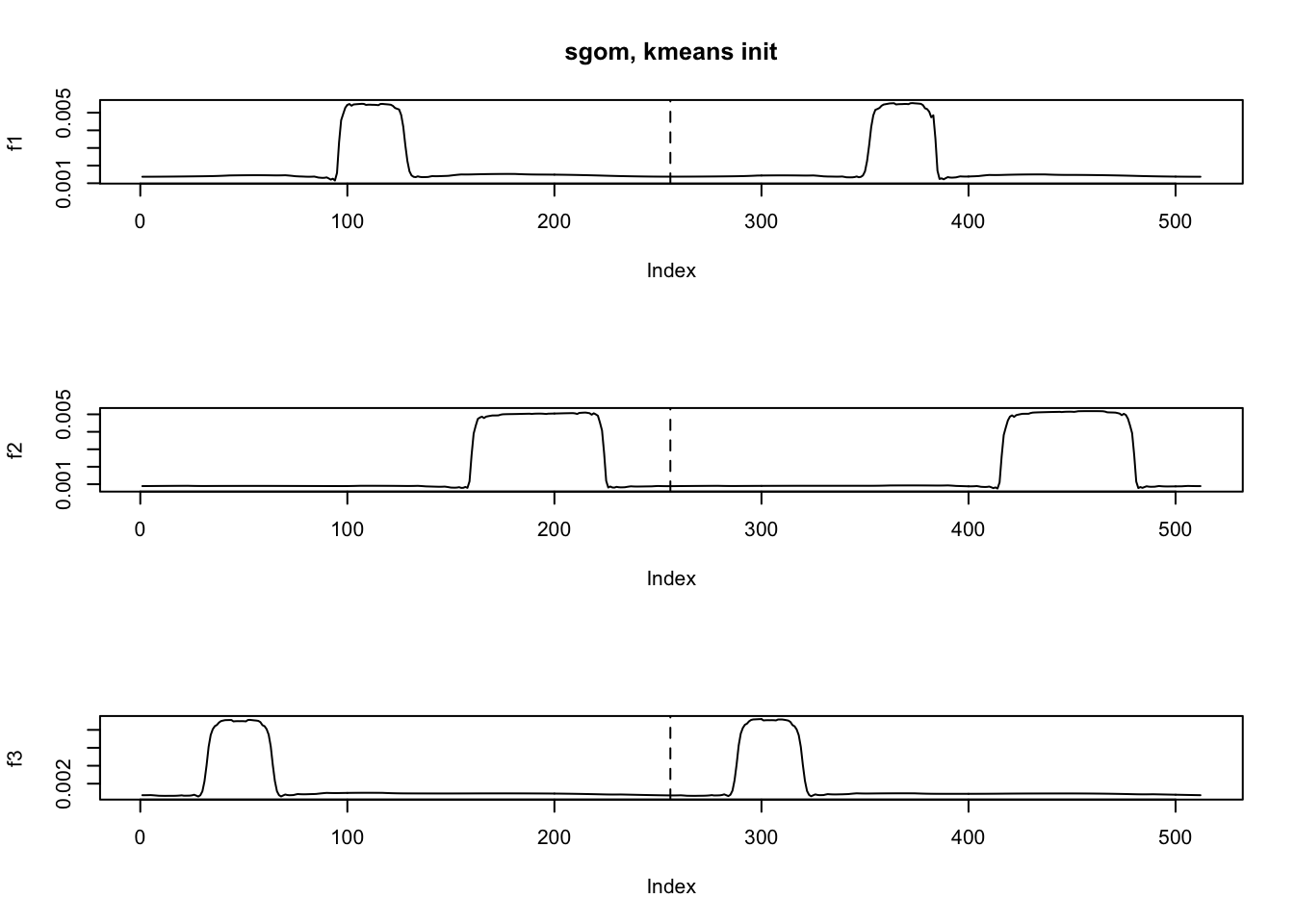
sessionInfo()R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS High Sierra 10.13.6
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] stm_1.0.0 tictoc_1.0.1 flashr_0.6-7 wavethresh_4.6.8
[5] MASS_7.3-53 testthat_3.0.0 devtools_2.3.2 usethis_1.6.3
[9] workflowr_1.6.2
loaded via a namespace (and not attached):
[1] genlasso_1.5 pkgload_1.1.0 splines_4.0.3 assertthat_0.2.1
[5] horseshoe_0.2.0 mixsqp_0.3-43 deconvolveR_1.2-1 yaml_2.2.1
[9] remotes_2.2.0 sessioninfo_1.1.1 ebnm_0.1-50 pillar_1.4.6
[13] backports_1.1.10 lattice_0.20-41 glue_1.4.2 digest_0.6.27
[17] promises_1.1.1 colorspace_1.4-1 htmltools_0.5.1.1 httpuv_1.5.4
[21] Matrix_1.2-18 plyr_1.8.6 pkgconfig_2.0.3 invgamma_1.1
[25] purrr_0.3.4 scales_1.1.1 processx_3.5.1 whisker_0.4
[29] later_1.1.0.1 git2r_0.27.1 tibble_3.0.4 generics_0.1.0
[33] ggplot2_3.3.2 ellipsis_0.3.1 withr_2.3.0 ashr_2.2-47
[37] cli_2.4.0 magrittr_2.0.1 crayon_1.3.4 memoise_1.1.0
[41] evaluate_0.14 ps_1.4.0 ebpm_0.0.1.3 fs_1.5.0
[45] truncnorm_1.0-8 pkgbuild_1.1.0 data.table_1.13.2 tools_4.0.3
[49] prettyunits_1.1.1 softImpute_1.4 REBayes_2.2 matrixStats_0.57.0
[53] lifecycle_1.0.0 stringr_1.4.0 trust_0.1-8 munsell_0.5.0
[57] irlba_2.3.3 callr_3.6.0 compiler_4.0.3 caTools_1.18.0
[61] rlang_0.4.10 grid_4.0.3 NNLM_0.4.4 rstudioapi_0.11
[65] igraph_1.2.6 bitops_1.0-6 rmarkdown_2.5 gtable_0.3.0
[69] DBI_1.1.0 reshape2_1.4.4 R6_2.4.1 knitr_1.30
[73] dplyr_1.0.5 rprojroot_1.3-2 smashr_1.2-9 desc_1.2.0
[77] stringi_1.5.3 SQUAREM_2020.5 Rcpp_1.0.5 vctrs_0.3.7
[81] tidyselect_1.1.0 xfun_0.18